Vamos iniciar com uma condição necessária para diferenciabilidade de uma função $ f: S \subset \mathbb{R}^n \rightarrow \mathbb{R}. $
Proposição: Se $ f $ é diferenciável no ponto $ a $ então $f$ é contínua neste ponto.
Demonstração: Para facilitar a notação suponhamos $ a=(a_1, a_2).$ Pela definição de diferenciabilidade
$ \lim_{(h, k) \rightarrow (0, 0)} \frac{f(a_1 + h, a_2+k ) -f(a_1, a_2) - \frac{\partial f}{\partial x} (a) .h - \frac{\partial f}{\partial y} (a). k }{\|(h, k)\|} =0. $
Se multiplicarmos por $ \|(h, k)\| $ o limite acima ainda converge para zero, ou seja
$ \lim_{(h, k) \rightarrow (0, 0)} f(a_1 + h, a_2+k ) -f(a_1, a_2) - \frac{\partial f}{\partial x} (a) .h - \frac{\partial f}{\partial y} (a). k = 0. $
Já que $ \ \lim_{(h, k) \rightarrow (0, 0)} \frac{\partial f}{\partial x} (a) .h + \frac{\partial f}{\partial y} (a). k= 0$, então $ \lim_{(h, k) \rightarrow (0, 0)} f(a_1 + h, a_2+k ) -f(a_1, a_2) = 0.$
O que implica
$ \lim_{(h, k) \rightarrow (0, 0)} f(a_1 + h, a_2 + k) = f(a_1, a_2).$
Como observamos anteriormente, as derivadas parciais de uma função podem existir sem que a função seja diferenciável no ponto.
Dado $ a $ no interior do domínio da função $ f $, quando as derivadas parciais existirem denotamos por gradiente de $ f $, o seguinte vetor:
$ \nabla(f) = \left(\frac{\partial f}{\partial x_1}(a), \cdots , \frac{\partial f}{\partial x_n}(a)\right) $
Proposição: Seja $ a $ no interior do domínio da $ f $ e suponhamos que todas as derivadas parciais existem numa vizinhança de $ a $ e contínua em $ a $. Então $ f $ é diferenciável no ponto $ a. $
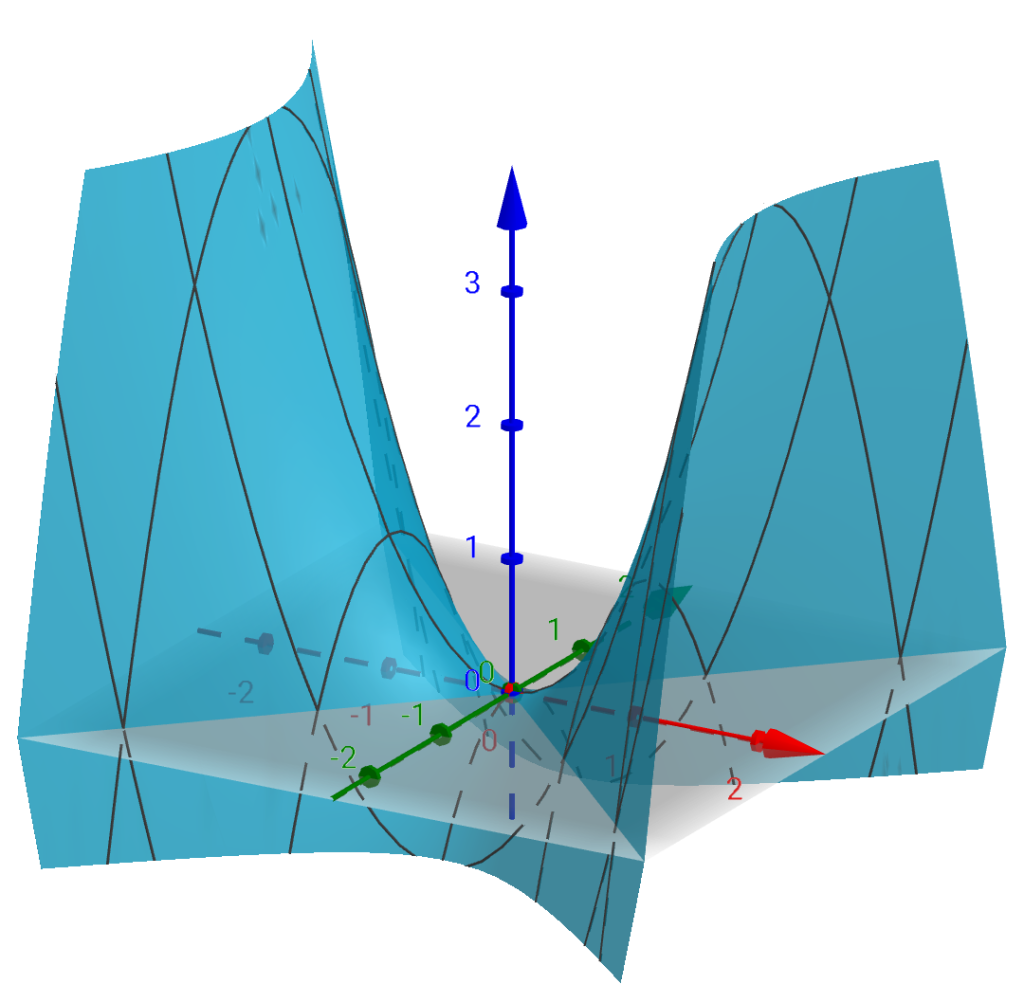
Exemplo: Considere $ f: \mathbb{R}^2 \rightarrow \mathbb{R}, f(x, y)= x^2 - y^2.$ Então no ponto $ a=(0, 0) $ temos $ \frac{\partial f}{\partial x}= 2x, \frac{\partial f}{\partial x} (a)=0 $ e
$ \frac{\partial f}{\partial y}= -2y, \frac{\partial f}{\partial y} (a)=0 $
e assim temos que ambas as derivadas parciais são funções contínuas no ponto $ a.$ Portanto pela proposição acima, $ f $ é diferenciável no ponto $ a $ e sua derivada é $ [0 0] $. O vetor gradiente no ponto $ (0, 0) $ também é $ (0, 0). $
Olhar geométrico
A equação do plano tangente ao gráfico da função é $ z=0.$ Na maioria dos exemplos quando analisamos o plano tangente, a superfície fica de um lado do plano. Porém, a superfície do gráfico desta função é um paraboloide hiperbólico (sela) e o plano tangente corta a superfície.
Compare este exemplo com função dada por $ f(x, y)= \frac{x^2y}{x^2 + y^2}$, que não existia plano tangente ao gráfico!
Lembremos o exemplo $ f(x, y) = \frac{x^2 y}{x^2 + y^2} $ e verificamos que as derivadas parciais não são contínuas no ponto $ (0, 0). $
Entretanto, uma função pode ser diferenciável sem que as derivadas parciais sejam contínuas.
Exemplo: $ f(x, y) = (x^2 + y^2) sen(\frac{1}{x^2+y^2}), (x, y) \neq (0,0) $ e $ f(0, 0 )= 0.$ Então verificamos que $ f $ é diferenciável em $ (0, 0) $, porém as derivadas parciais não são contínuas em $ (0, 0). $
Derivadas direcionais
Até agora definimos derivadas parciais $ \frac{\partial f}{\partial x_i}, i=1, \cdots , n$ e também a derivada como uma transformação linear. Já mencionamos que a derivada de uma função $ f: \mathbb{R}^n \rightarrow \mathbb{R}$ em cada ponto onde a função é diferenciável é uma matriz $ 1\times n $ cujas entradas são exatamente as derivada parciais. Isto tem uma justificativa:
Pela definição da derivada no ponto $ a = (a_1, \cdots, a_n) $, se $ [d_1, \cdots, d_n] $ representar a matriz da derivada no ponto $ a: $
$ \lim_{h \rightarrow 0} \frac{f(a+h)-f(a) - (d_1h_1+ \cdots + d_n h_n) }{\|h\|} = 0. $ Lembrem que $ h= (h_1, \cdots, h_n)$ e a convergência $ h \rightarrow 0 $ está acontecendo em $ \mathbb{R}^n. $
Portanto se substituirmos $ h= (0, \cdots, h_i, \cdots, 0)$ (convergindo apenas na $ i $-ésima coordenada) teremos:
$ \lim_{h_i \rightarrow 0} \frac{f(a_1, \cdots, a_i+h_i, \cdots)-f(a_1, \cdots, a_n) - (d_i h_i) }{\|h\|} = 0. $
Isto implica que
$ d_i = \frac{\partial f}{\partial x_i} (a). $
Como falamos anteriormente, as derivadas parciais são taxas de variação da função nas direções dos eixos das coordenadas. Entretanto, podemos calcular a taxa de variação de uma função em outras direções.
Considere $ v \in \mathbb{R}^n$ um vetor com norma 1 ( $ \|v\|=1. $ Então definimos a derivada na direção $ v $ como:
$ D_v f(a) = \lim_{t \rightarrow 0} \frac{f(a+tv) - f(a)}{t} $ e lembramos que as derivadas parciais $ \frac{\partial f}{\partial x_i}(a) $ são calculadas quando $ v = e_i = (0, \cdots, 1, \cdots, 0) $ onde $ 1 $ está na posição $ i. $
Exemplo: Calcule a derivada direcional $ D_v f (a) $ onde $ f(x, y) =x^2 + y^2 , v=(-1, 0)$ e $ a=(0, 1). $
Por definição precisamos calcular
$ \lim_{t \rightarrow 0} \frac{f(a+tv)- f(a)}{t} = \lim_{t \rightarrow 0} \frac{(-t)^2 + 1 -1}{t} =0. $
Existe uma forma simples para calcular derivadas direcionais a partir da derivada. De fato, $ D_v f(a) = \nabla f(a) \cdot v$, onde $ \nabla f$ é o vetor gradiente e o produto é o produto interno entre vetores. Para isto basta observar a definição da derivada da função no ponto $ a.$ Se $ \nabla f(a) = (d_1, \cdots, d_n) $ então já que $ \|v\|=1$:
$ \lim_{t \rightarrow 0} \frac{f(a+tv) - f(a) - \nabla f(a) . tv}{ t} =0$ e isto mostra que as derivadas direcionais são exatamente o que foi afirmado anteriormente.
Um resultado importante sobre curvas de nível:
Teorema: Seja $ f: \mathbb{R}^2 \rightarrow \mathbb{R}$ uma função diferenciável. Então o vetor gradiente no ponto $ a $ do domínio é ortogonal a curva de nível passando pelo ponto $ a. $
Vamos demonstrar depois de falar da regra de cadeia, porém a ideia é a seguinte: Ao longo da curva de nível a função é constante, “Portanto sua derivada direcional com respeito ao vetor tangente a curva de nível tem que ser zero”. Isto significa que o produto escalar entre o gradiente e vetor tangente da curva é zero, que por sua vez implica ortogonalidade entre eles.