Uma curva parametrizada é uma função $ \gamma: I \rightarrow \mathbb{R}^n $ onde $ I \subset \mathbb{R} $ é um intervalo. Geralmente interpretamos $ \gamma(t) $ como “posição” de uma partícula em $ \mathbb{R}^n $ no momento $ t $.

Exemplo: Considere duas partículas no espaço 3-dimensional movimentando conforme lei do Newton (atração entre elas). A posição de cada partícula é determinada por 3 coordenadas (que depende do tempo $ t $). Portanto $ \gamma_1, \gamma_2 : I \rightarrow \mathbb{R}^3 $ representam posição de cada partícula. Podemos juntar as duas e descrever a configuração do sistema de duas partículas como única função $ \Gamma: I \rightarrow \mathbb{R}^6. $ Ou seja, a configuração temporal das posições de k partículas em movimento no espaço 3-dimensional pode ser representada por uma curva no espaço $ \mathbb{R}^{3k}. $

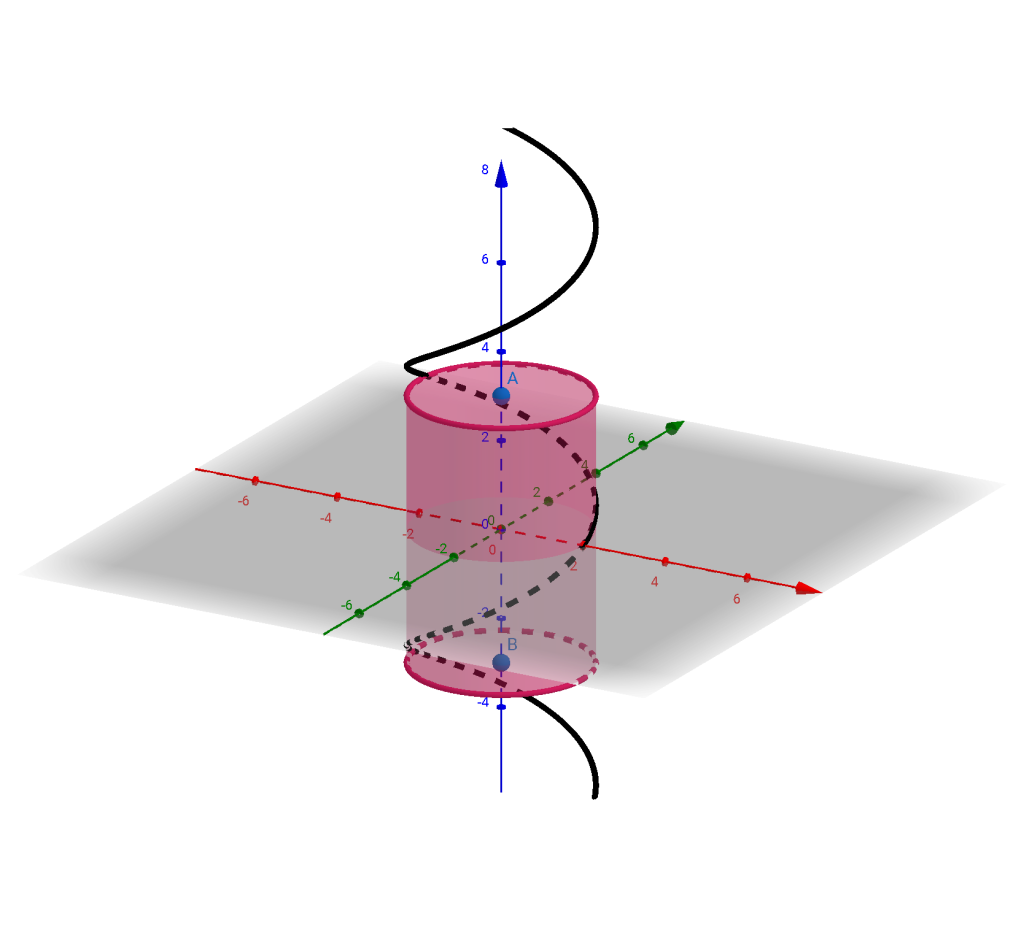
Exemplo: Considere $ \gamma: \mathbb{R} \rightarrow \mathbb{R}^3, \gamma(t)=(a cos(t), a sen(t), bt) , t \in \mathbb{R}.$ Essa é parametrização de uma curva que cujo traço espirala sobre cilíndrio $ x^2+y^2=a^2 $.

Duas curvas $ \gamma_1, \gamma_2 $ podem ter o mesmo traço. Por exemplo $ \gamma_1(t)= (cos(t), sen(t)), t \in [0, 2\pi] $ , $ \gamma_2(t)= (sen(t), cos(t), t \in [0, 2\pi]) $ , $ \gamma_3(t)= (cos(2t), sen(2t), t \in [0, \pi]) $ e $ \gamma_4(t)= (cos(2t), sen(2t), t \in [0, 2\pi])$

todas tem o mesmo traço. O traço de todas as curvas é o círculo unitário $ x^2+y^2=1$ no plano. Entretanto, nos casos $ \gamma_1, \gamma_2, \gamma_3 $ a partícula gira apenas uma vez sobre círculo, enquanto no caso de $ \gamma_4 $ dá duas voltas.

Enquanto $ \gamma_1 $ inicia no tempo $ t=0 $ no ponto $ (1, 0) $ e traça no sentido anti-horário o círculo, a partícula seguindo regra definida por $ \gamma_2 $ inicia no ponto $ (0, 1) $ e vai no sentido horário.

A curva $ \gamma_3 $ como $ \gamma_1 $ inicia no ponto $ (1, 0) $ porém percorre o circulo na metade do tempo (i. e $ \pi $). de fato a velocidade da partícula dobrou!

Para uma curva $ \gamma: I \rightarrow \mathbb{R}^n $ podemos discutir continuidade e diferenciabilidade também.

Continuidade: Se $ t_0 \in I $, então a curva é contínua no ponto $ t=t_0 $ se para qualquer $ \epsilon > 0 $ exista $ \delta > 0 $ tal que se $ |t-t_0| \leq \delta $ então $ |\gamma(t)-\gamma(t_0)| \leq \epsilon. $ Observe que essa definição é como continuidade no cálculo 1, apenas observem que $ \gamma(t) - \gamma(t_0) $ é um vetor em $ \mathbb{R}^n $ e $ |\gamma(t)-\gamma(t_0)|$ representa a norma deste vetor.

Lembramos que se $ \gamma(t)= (\gamma_1(t), \gamma_2(t), \cdots, \gamma_n(t)) $ e $ \gamma(t_0)= (\gamma_1(t_0), \gamma_2(t_0), \cdots, \gamma_n(t_0)) $ então:

$ \|\gamma(t) - \gamma(t_0) \|= \sqrt{(\gamma_1(t)-\gamma_1(t_0))^2 + \cdots (\gamma_n(t)-\gamma_n(t_0))^2}$

Por outro lado

$ |\gamma_i(t) - \gamma_i(t_0)| \leq \|\gamma(t) - \gamma(t_0)\| \leq \sqrt{n} max_{i=1,\cdots, n} |\gamma_i(t)-\gamma_i(t_0)|$

a desigualdade esquerda vale para todo $ 1 \leq i \leq n.$

Conclusão: A curva $ \gamma: I \rightarrow \mathbb{R}^n $ é contínua no ponto $ t_0 $ se somente se todas as funções $ \gamma_i : I \rightarrow \mathbb{R} $ são contínuas no ponto $ t_0. $

De uma forma similar podemos definir noção de limite e podemos provar que $ \lim_{t \rightarrow t_0} \gamma(t) = L= (l_1, \cdots, l_n) \in \mathbb{R}^n $ se somente se $ \lim_{t \rightarrow t_0} \gamma_i(t) = l_i $ para todo $ 1 \leq i \leq n. $

Diferenciabilidade:

De uma forma similar as funções reais podemos definir a derivada para uma curva: Uma curva $ \gamma: I \rightarrow \mathbb{R}^n $ é diferenciável no ponto $ t=t_0 $ se

$ \lim_{h \rightarrow 0} \frac{\gamma(t_0+h) - \gamma(t_0}{h} $

existir e este limite é denotado por $ \gamma^{'}(t_0). $ Observem que $ \gamma^{'}(t_0) $ é um vetor em $ \mathbb{R}^n. $ Este vetor é o vetor da velocidade.

É bom ressaltar que não podemos misturar o traço de uma curva (a figura geométrica) com ela, que é uma função.

Novamente podemos demonstrar que $ \gamma $ é diferenciável em $ t=t_0 $ se somente se $ \gamma_i : I \rightarrow \mathbb{R} $ forem diferenciáveis em $ t_0 $ para todo $ 1 \leq i \leq n. $

Exemplo: Considere $ \gamma: \mathbb{R} \rightarrow \mathbb{R}^2 $ tal que $ \gamma(t)= (t^3, t^2). $ O traço desta curva é formado por pontos $ (x, y), x=t^3, y=t^2 $ Observe que $ \gamma^{'}(t) = (3t^2, 2t) $ e no ponto $ t=0 $ temos $ \gamma^{'}(0)=(0, 0). $

Veja o traço da curva abaixo e discute o bico que aparece no traço da curva e que mesmo assim a curva tem derivada no ponto $ t=0. $ Isto mostra que não devemos traço de uma curva com gráfico da função.

Dada uma função $ \gamma: I \rightarrow \mathbb{R}^n$ escrevemos

$ \gamma(t) = (\gamma_1(t), \cdots, \gamma_n(t)) $. Se $ \gamma $ for diferenciável no ponto $ t=t_0 $ então

$ \gamma^{'}(t_0)= (\gamma_1^{'}(t_0), \cdots, \gamma_n^{'}(t_0)) $ é vetor da derivada. Na mecânica, se $ \gamma $ representar o movimento de uma partícula, então $ \gamma^{'}(t) $ é a velocidade no momento $ t. $

Reparametrização:

Seja $ \gamma: [a, b] \rightarrow \mathbb{R}^n $ uma curva diferenciável no $ \mathbb{R}^n$ (nos pontos extremais consideramos apenas derivada lateral!) e $ \alpha: [c, d] \rightarrow [a,b] $ uma função diferenciável com derivada contínua. Suponhamos que $ \alpha^{'}(t) >0 $, então podemos verificar que

$ \eta: [c, d] \rightarrow \mathbb{R}^n $ também é uma curva diferenciável e seu traço coincide com traço de $ \gamma. $

Usando regra de cadeia podemos verificar que

$ \eta^{'}(t) = (\gamma_1^{'}(\alpha(t)) \alpha^{'}(t), \cdots, \gamma_1^{'}(\alpha(t)) \alpha^{'}(t) ) = $

$ = \alpha^{'}(t) \gamma^{'}(\alpha(t)).$

Ou seja a velocidade de $ \eta$ no momento $ t $ múltiplo positivo da velocidade de $ \gamma $ no momento $ \alpha(t) $.

A curva $ eta $ é uma reparametrização de $ \gamma $ preservando a orientação.

Se $ \alpha^{'}(t) < 0 $ para todo $ t \in [c, d] $ então teremos uma reparametrização invertendo orientação.

Algumas propriedades da derivada:

Colocamos como exercício:

Sejam $ \gamma, \eta: I \rightarrow \mathbb{R}^n $ diferenciáveis, então: $ (\gamma.\eta)^{'}(t) = \gamma^{'}(t) \eta(t) + \gamma(t) \eta^{'}(t) $ , lembrando que $ \gamma(t). \eta(t)$ é o produto escalar entre dois vetores.

2. Sejam $ \gamma: I \rightarrow \mathbb{R}^n $ e $ f : I \rightarrow \mathbb{R}$ diferenciáveis, então $ f\gamma: I \rightarrow \mathbb{R}$ é diferenciável e

$(f \gamma)^{'}(t) = f(t) \gamma^{'}(t) + f^{'}(t) \gamma(t).$

3. Sejam $ \gamma, \eta: I \rightarrow \mathbb{R}^3 $ diferenciáveis, então, $ \gamma \times \eta: I \rightarrow \mathbb{R}$ é diferenciável e

$ (\gamma \times \eta)^{'}(t) = \gamma^{'}(t) \times \eta(t) + \gamma(t) \times \eta^{'}(t). $