This is an old revision of the document!

---

Vamos iniciar com uma condição necessária para diferenciabilidade de uma função $ f: S \subset \mathbb{R}^n \rightarrow \mathbb{R}. $

Proposição: Se $ f $ é diferenciável no ponto $ a $ então é contínua neste ponto.

Demonstração: Para facilitar a notação suponhamos $ a=(a_1, a_2).$ Pela definição de diferenciabilidade

$ \lim_{(h, k) \rightarrow (0, 0)} \frac{f(a_1 + h, a_2+k ) -f(a_1, a_2) - \frac{\partial f}{\partial x} (a) .h - \frac{\partial f}{\partial y} (a). k }{\|(h, k)\|} =0. $

Se multiplicarmos por $ \|(h, k)\| $ o limite acima ainda converge ao zero, ou seja

$ \lim_{(h, k) \rightarrow (0, 0)} f(a_1 + h, a_2+k ) -f(a_1, a_2) - \frac{\partial f}{\partial x} (a) .h - \frac{\partial f}{\partial y} (a). k = 0. $

Já que $ \ \lim_{(h, k) \rightarrow (0, 0)} \frac{\partial f}{\partial x} (a) .h + \frac{\partial f}{\partial y} (a). k= 0$

então $ \lim_{(h, k) \rightarrow (0, 0)} f(a_1 + h, a_2+k ) -f(a_1, a_2) = 0.$

que implica

$ \lim_{(h, k) \rightarrow (0, 0)} f(a_1 + h, a_2 + k) = f(a_1, a_2).$

Como observamos anteriormente as derivadas parciais de uma função podem existir sem que a função seja diferenciável no ponto.

Dado $ a $ no interior do domínio da função $ f $ quando as derivadas parciais existirem denotamos por gradiente de $ f $, o seguinte vetor:

$ \nabla(f) = (\frac{\partial f}{\partial x_1}(a), \cdots , \frac{\partial f}{\partial x_n}(a)) $

Proposição: Seja $ a $ no interior do domínio da $ f $ e todas as derivadas parciais existirem numa vizinhança de $ a $ e contínua em $ a $ então $ f $ é diferenciável no ponto $ a. $

Exemplo: Considere $ f: \mathbb{R}^2 \rightarrow \mathbb{R}, f(x, y)= x^2 - y^2.$ Então no ponto $ a=(0, 0) $ temos $ \frac{\partial f}{\partial x}= 2x, \frac{\partial f}{\partial x} (a)=0 $ e

$ \frac{\partial f}{\partial y}= -2y, \frac{\partial f}{\partial y} (a)=0 $

e assim temos que ambas as derivadas parciais são funções contínuas no ponto $ a.$ Portanto pela proposição acima, $ f $ é diferenciável no ponto $ a $ e sua derivada é $ [0 0] $. O vetor gradiente no ponto $ (0, 0) $ também é $ (0, 0). $

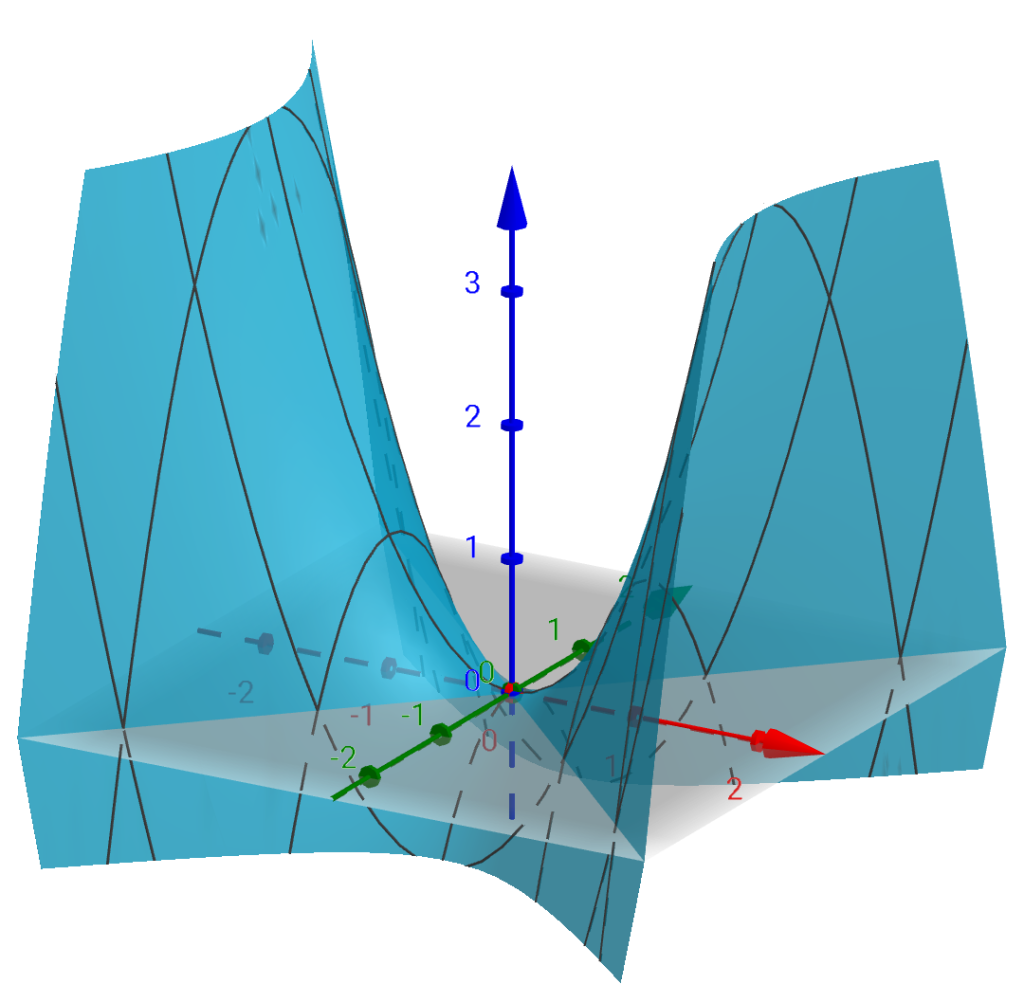
Olhar geométrico: A equação do plano tangente ao gráfico da função é $ z=0.$ Em maioria dos exemplos quando analisamos o plano tangente, a superfície fica de um lado do plano. Porém, a superfície do gráfico desta função é paraboloide hiperbólico (sela) e o plano tangente corta a superfície.

Compare este exemplo com função dada por $ f(x, y)= \frac{x^2y}{x^2 + y^2}$ que não existia plano tangente ao gráfico!

Lembramos o exemplo $ f(x, y) = \frac{x^2 y}{x^2 + y^2} $ vamos verificar que as derivadas parciais não são contínua no ponto $ (0, 0). $

Entretanto, uma função pode ser diferenciável sem que as derivadas parciais sejam contínuas.

Exemplo: $ f(x, y) = (x^2 + y^2) sen(\frac{1}{x^2+y^2}), (x, y) \neq (0,0) $ e $ f(0, 0 )= 0.$ Então verificamos que $ f $ é diferenciável em $ (0, 0) $ porém as derivadas parciais não são contínuas em $ (0, 0). $

Derivadas direcionais:

Até agora definimos derivadas parciais $ \frac{\partial f}{\partial x_i}, i=1, \cdots , n$ e também derivada como uma transformação linear. Já meniconamos que a derivada de uma função $ f: \mathbb{R}^n \rightarrow \mathbb{R}$ em cada ponto onde a função é diferenciável é uma matriz $ 1\times n $ cujas entradas são exatamente as derivada sparciais. Isto tem uma justificativa:

Pela definição da derivada no ponto $ a = (a_1, \cdots, a_n) $, se $ [d_1, \cdots, d_n] $ representar a matriz da derivada no ponto $ a: $

$ \lim_{h \rightarrow 0} \frac{f(a+h)-f(a) - (d_1h_1+ \cdots + d_n h_n) }{\|h\|} = 0. $ Lembrem que $ h= (h_1, \cdots, h_n)$ e convergência $ h \rightarrow 0 $ está acontecendo em $ \mathbb{R}^n. $

Portanto se substituirmos $ h= (0, \cdots, h_i, \cdots, 0)$ (convergir apenas na $ i $ ésima coordenada) teremos

$ \lim_{h_i \rightarrow 0} \frac{f(a_1, \cdots, a_i+h_i, \cdots)-f(a_1, \cdots, a_n) - (d_i h_i) }{\|h\|} = 0. $ Isto implica que

$ d_i = \frac{\partial f}{\partial x_i} (a). $

Como falamos anteriormente, as derivadas parciais são taxas de variação da função nas direções dos eixos das coordenadas. Entretanto, podemos calcular taxa de variação de uma função em outras direções.

Considere $ v \in \mathbb{R}^n$ um vetor com norma um ( $ \|v\|=1. $ Então definimos a derivada na direção $ v $ como:

$ D_v f(a) = \lim_{t \rightarrow 0} \frac{f(a+tv) - f(a)}{t} $ e lembramos que as derivadas parciais $ \frac{\partial f}{\partial x_i}(a) $ são calculadas quando $ v = e_i = (0, \cdots, 1, \cdots, 0) $ onde $ 1 $ está na posição $ i. $

Exemplo: Calcule a derivada direcional $ D_v f (a) $ onde $ f(x, y) =x^2 + y^2 , v=(-1, 0)$ e $ a=(0, 1). $

Por definição precisamos calcular

$ \lim_{t \rightarrow 0} \frac{f(a+tv)- f(a)}{t} = \lim_{t \rightarrow 0} \frac{(-t)^2 + 1 -1}{t} =0. $

Existe uma forma simples para calcular derivadas direcionais a partir da derivada. De fato

$ D_v f(a) = \nabla f(a) . v$ onde $ \nabla f$ é o vetor gradiente e o produto é produto interno entre vetores. Para isto basta observar a definição da derivada da função no ponto $ a.$ Se $ \nabla f(a) = (d_1, \cdots, d_n) $ então já que $ \|v\|=1$:

$ \lim_{t \rightarrow 0} \frac{f(a+tv) - f(a) - \nabla f(a) . tv}{ t} =0$ e isto mostra que a derivada direcionais é exatamente o que foi afirmada.

Um resultado importante sobre curvas de nível:

Teorema: Seja $ f: \mathbb{R}^2 \rightarrow \mathbb{R}$ uma função diferenciável. Então o vetor gradiente no ponto $ a $ do domnínio é ortogonal `a curva de nível passando pelo ponto $ a. $

(vamos demonstrar depois de falar da regra de cadeia - veja ) Porém a ideia é seguinte: Ao longo da curva de nível a função é constante. “Portanto sua derivada direcional com respeito ao vetor tangente a curva de nível tem que ser zero” Isto significa que o produto escalar entre gradiente e vetor tangente da curva é zero que por sua vez implica ortogonalidade.