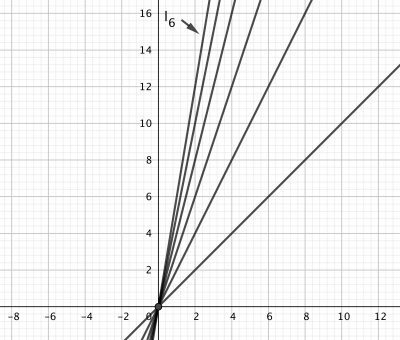Chegou a hora de falar como somar dois números irracionais! Dado dois números a e b. se eles são racionais na escola aprendemos como somá-los. Mas como somar $ \sqrt{2}$ e $ \sqrt{3}?$

Precisamos lembrar que cada número irracional tem uma representação por decimais. Seja $ a_n$ e $b_n$ o truncamento por n digitos da expansão decimal de a e b. Lembrando que assim temos aproximação de $a$ e $b$ por um erro de no máximo $ 10^{-n}.$ Portanto se considerarmos $ a_n + b_n$ (soma de dois números racionais) teremos um resultado que no máximo tem um erro $ 2 \times 10^{-n}$ até a soma “verdadeira” de a e b. Assim aumentando $n$, teremos resultados cada vez mais próximo a valor de $ a+b$.

Se pensar um pouco, vamos ver que para produto ou divisão de dois números irracionais, o método de aproximar por racionais não é tão trivial quanto a soma.

o exemplo de $ a_n$ acima é exemplo de uma sequência de números. Uma sequência de números reais geralmente é denotado por $ (a_n)_{n \in \mathbb{N}}, a_n \in \mathbb{R}$. Porém podemos encontrar sequnências como $ (a_n)_{n \geq k} $ ou $ (a_n)_{n=k}^{\infty}$.

Exemplo: Seja $ a_n = n+\frac{1}{n},$ então os elementos desta sequência crescem com índice (n) , i.e $ a_n \leq a_{n+1}$ e os elementos desta sequência não se acumulam perto de nenhum número.

Em geral no cálculo 1 trabalhamos com sequências que cada elemento delas é um número real. Porém, uma sequência em E (um conjunto qualquer e não necessariamente $ \mathbb{R}$) é uma função de $ \mathbb{N}$ em E.

por exemplo podemos considerar sequência de escadas que “aproximam” a hipotenusa de um triângulo retangular como na pagina Cálculo: vamos quebrá-lo!

Outro exemplo (sequência de retas!): seja $ l_n$ uma sequência de retas que passam pela origem com inclinação n. Os elementos desta sequência são retas que quando o índice n cresce os elementos ficam mais próximo a reta vertical. Podemos considerar essa sequência como sequência de funções também. Aqui $ f_n$ pode ser considerado $n$ 'esimo elemento da sequência, onde $ f_n$ é a função com regra $ f_n(x)=nx, x\in \mathbb{R}.$

Chegamos a um conceito bastante interessante. Já encontramos uma vez este conceito de convergência quando falamos de números irracionais e sua aproximação por números racionais a partir de sua expansão decimal. Porém a sequência de aproximações por decimais é uma sequência muito bem comportada e “tame”. A partir de agora quando falamos sequência, referimos sequência de números. A noção de convergência para números já é suficientemente delicada.

Seja $ (a_n)_{n \in \mathbb{N}} $ uma sequência real, então dizemos que a sequência converge, se existir $ a_*$ tal que para todo $ \epsilon > 0$ exista N, tal que $ |a_n - a_*| \leq \epsilon$ para todo $ n > N.$

Observe que N em geral depende do $ \epsilon.$

Vamos falar em português!: Para qualquer precisão $ \epsilon$, existe N tal que a partir de N, todo elemento da sequência $ a_n, n > N$ é $ \epsilon$ próximo a $ a_*$, ou seja para um computador com precisão $ \epsilon$ , todos os elementos $ a_n, n > N$ são iguais a $ a_*$.

Exemplo 1.

Considere a sequência -1, 1, -1, 1, -1,…. i.e $ a_n = (-1)^n$. Essa sequência não converge a nenhum limite. Vamos demonstrar por absurdo. Suponhamos que exista um limite L para tal sequência. Portanto pela definição Para qualquer $ \epsilon > 0 $ existe $ N \in \mathbb{N}$ tal que para todo $ n > N$ temos $ |a_n -L|\leq \epsilon$. Se colocarmos $ \epsilon = 1/2$ então deveria existir algum $ N$ tal que para todo $ n > N$ teriamos $ |a_n - L| \leq 1/2$.

Portanto pela desigualdade triangular teriamos $ |a_n - a_{n+1}| \leq |a_n -L|+|L - a_{n+1}| \leq 1/2 + 1/2 =1.$ Isto é um absurdo, pois $ |a_n - a_{n+1}| =2$ para todo n.

Exemplo2 :

Seja $ a_n = \frac{1}{n}$. Essa sequência converge a 0. Escrevemos

$ \lim_{n \rightarrow \infty} a_n = 0.$

De fato, se $ \epsilon > 0$ é arbitrário, podemos escolher sempre um número $ N$ tal que $ N > \frac{1}{\epsilon} $ ou seja $ \frac{1}{N} < \epsilon$ e portanto para todo $ n \geq N$ temos

$ |a_n - 0| = |\frac{1}{n} - 0| = \frac{1}{n} \leq \frac{1}{N} < \epsilon.$

O seguinte teorema é uma ferramenta fundamental para calcular limites.

Não ignorem o poder do teorema acima!

Você precisa usar ele diversas vezes e é necessário aplicar corretamente.por exemplo, considere $ a_n = \frac{(-1)^n}{n}.$ Essa sequência converge a zero, mas não podemos simplemente considerar essa sequência como divisão de duas sequências $ (-1)^n$ e $n$ e calcular o limite. Pois $ (-1)^n$ não possui limite. Porém escolhendo N, exatamente como caso da sequência $ 1/n$ teremos

$ |a_n - 0| = |\frac{(-1)^n}{n} - 0| = \frac{1}{n} \leq \frac{1}{N} < \epsilon. $

e isto mostra que o limite é zero.

Exemplo: Considere $ a_n = 1/n$ e $ b_n= 2/n$. O que acham do limite de $ c_n = a_n / b_n$. Claro que $ c_n = 1/2$ para todo n e portanto $ \lim_{n \rightarrow \infty} c_n = \frac{1}{2}.$ Porém não podemos usar o teorema acima, pois $ b_* = 0.$

Vamos provar o teorema:

item (1): Vamos utilizar uma linguagem computacional. Seja $ a_n$ uma aproximação de $ a_*$ e $ |a_n - a_*|$ será chamado de erro de aproximação. Agora se considerarmos $ a_n+b_n$ como uma aproximação de $ a_* + b_*$ então qual será o erro de aproximação?

Suponhamos $ \delta= a_* - a_n, \delta^{'} = a_* - b_n$. Então

$ (a_* + b_*) - (a_n + b_n) = (a_* - a_n) + (b_* -b_n)$ e portanto

$ |(a_* + b_*) - (a_n + b_n)| \leq |\delta| + |\delta^{'}|$ ou seja se considerarmos $ a_n + b_n$ como uma aproximação de $ a_* + b_*$ o erro de aproximação não é maior do que a soma dos erros de aproximações. Portanto se desejarmos aproximar $ a_* + b_*$ com um erro menor do que $ \epsilon$ é suficiente usar a convergência de $ a_n$ e achar $ N_1$ tal que para $ n \geq N_1$

$ |a_* - a_n| \leq \frac{\epsilon}{2}$

Da mesma forma existe $ N_2$ tal que para todo $ n \geq N_2$ teremos

$ |b_* - b_n| \leq \frac{\epsilon}{2}.$

Agora se escolhermos N, um número inteiro maior do que $ N_1$ e $ N_2$ então para todo $ n \geq N$ teremos

$ |\delta| \leq \epsilon /2, |\delta^{'}| \leq \epsilon /2$ e portanto o erro de aproximação de $ a_* + b_*$ por $ a_n + b_n$ para $ n \geq N$ será menor do que $ \epsilon.$

Agora vamos analisar como será a prova da parte (2) do teorema: qual será o erro de aproximação de $ a_*b_*$ por $ a_n b_n$, se o erro de aproximação de $ a_*$ por $ a_n$ é igual a $ \delta$ e da aproximação de $ b_*$ é $ \delta^{'}$:

$ a_*b_* - a_n b_n = (a_n + \delta)(b_n + \delta^{'}) - a_nb_n = a_n \delta^{'} + b_n \delta + \delta \delta^{'}.$

claro que se $ \delta, \delta^{'}$ forem pequenos então $ \delta \delta^{'}$ também é um número pequeno, mas $ a_n \delta^{'}$ ou $ b_n \delta$ podem não ser pequenos. Para continuar vamos precisar de seguinte lema:

Lema: Seja $ z_n$ uma sequência que converge a $ z_*$. Então existe um número $ K $ tal que para todo $ n$, temos $ |z_n| < K$ e além disto $ |z_*| < K.$

Vamos usa o lema acima para terminar a demonstração do item (2) do teorema.

Primeiramente observe que

$ |a_*b_* - a_nb_n| = (a_*b_* - a_*b_n) + (a_*b_n -a_nb_n)$ e portanto

Seja $ \epsilon > 0$ um número real e que queremos aproximar $ a_*b_*$ com precisão $ \epsilon$ por sequência $ a_n b_n.$ Pelo lema anterior existe K e L tais que

$ |a_n| < K, |a_*| < K$ e da mesma forma $ |b_n| < L , |b_*| < L.$

Por outro lado sabemos pela convergência das sequências $ a_n$ e $ b_n$ que existem $ N_1, N_2$ tais que para $ n \geq N_1$ temos

$ |a_* - a_n| \leq \frac{\epsilon}{2L}$

e por outro lado para $ n \geq N_2$ teremos

$ |b_* - b_n| \leq \frac{\epsilon}{2K}$

portanto se escolhermos N maior do que ambos os números $ N_1$ e $ N_2$ então para todo $ n \geq N$ teremos

$ |a_*b_* - a_n b_n| \leq K \frac{\epsilon}{2K} + L \frac{\epsilon}{2L} = \epsilon.$

 Um belo exemplo

Seja $ a= 487.r_1r_2r_3\cdots , b = 3. s_1s_2s_3\cdots$ onde $ r_n$ e $ s_n$ são computáveis com algum esforço! Queremos escolher n tal que se

$ a_n = 487.r_1r_2r_3\cdots r_n$ e $ b_n = 3. s_1s_2s_3\cdots s_n $ então a diferença entre $ a_nb_n$ e ab seja menor do que $ 10^{-5}.$ Isto é, num computador com precisão $10^{-5}$ $a_n b_n$ é o memso que $ab.$

observem que pela desigualdade maravilhosa acima e o fato de que $ |a-a_n| \leq 10^{-n}, |b-b_n| \leq 10^{-n}$ temos $ |ab - a_n b_n| \leq (K+L) 10^{-n}$ onde $K$ e $L$ são estimativas superiores para $ a_n, b_n$.

portanto, se colocarmos $K=488$ e $L=4$ temos

$ |ab - a_n b_n| \leq 492 \times 10^{-n}$.

Agora, para que essa diferença seja menor do que $ 10^{-5}$ basta escolher n tal que $ 492 \times 10^{-n} < 10^{-5}$ ou seja $ 492 < 10^{n-5}$. O menor n que satisfaz essa desigualdade é n=8. Portanto se usarmos 8 dígitos decimais de a e b, a aproximação de ab terá precisão de pelo menos $ 10^{-5}.$ LEGAL, né?