Para começar vamos a etimologia: Cálculo significa “pedrinha, seixo”. Antigamente as pessoas usavam pedrinhas para fazer “cálculos”!

É bom saber que essas pedrinhas (cálculos) foram meios para que Armstrong pudesse dizer: One small step for a man, one giant leap for mankind!

Decifra a Piada abaixo (do Livro Infinite Powers, Strogatz):

Dr. Foreman: The kid was just taking his AP (advance placement) calculus exam when all of a sudden, he got nauseous and disoriented!

Dr. House: That is the way calculus presents!

Entretanto, é bom frisar que inicialmente Leibniz usava “um cálculo” ou até “meu cálculo” para denotar os algoritmos e contas que estava fazendo.

É contado sob a forma de uma corrida entre Aquiles e uma tartaruga. Aquiles, herói grego, e a tartaruga decidem apostar uma corrida. Como a velocidade de Aquiles é maior que a da tartaruga, esta recebe uma vantagem, começando a corrida um trecho na frente da linha de largada de Aquiles. Aquiles nunca passa à tartaruga, pois quando ele chegar à posição inicial A da tartaruga, esta encontra-se mais a frente, numa outra posição B. Quando Aquiles chegar a B, a tartaruga não está mais lá, pois avançou para uma nova posição C e assim sucessivamente, ad infinito.

Em termos matemáticos, seria dizer que o limite, com o espaço entre a tartaruga e Aquiles tendendo a 0, do espaço de Aquiles, é a tartaruga. Ou seja, ele virtualmente alcança a tartaruga, mas nessa linha de raciocínio, não importa quanto tempo se passe, Aquiles nunca alcançará a tartaruga nem, portanto, poderá ultrapassá-la.

Só que não! por quê? o que você acha sobre este paradoxo? De fato é correto que existem infinitas etapas para que o Aquiles chegue a tartaruga, mas o ponto é que isto ocorre no tempo finito!!

.

De fato o cálculo é formado por duas artes: Arte de quebrar em pedaços muito pequenos e depois juntar os cacos! vamos ver um exemplo de Archimedes:

Relação entre área e perímetro de um círculo:

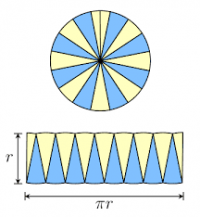
Se cortarmos uma pizza entre muitos amigos e em vez de comer re arranjamos os pedaços como a figura, a medida que número de amigos aumenta a figura re-arranjada fica “mais similar a um retângulo”cujos lados medem r (raio) e P (perímetro). Já que ninguém comeu a pizza neste processo a área é igual, ou seja

 $ A \sim \frac{1}{2}Pr $

Fácil né?  De jeito nenhum!

Realmente a área é igual a metade do perímetro vez o raio do círculo? Já que nunca o re-arranjo não será igual a um retângulo, podemos aceitar a igualdade? Será que isto não passa de um delírio e mágica?

Para valorizar um pouco mais este duelo entre igualdade ou aproximação vamos observar seguinte “fake news”: O Pitágoras estava errado!

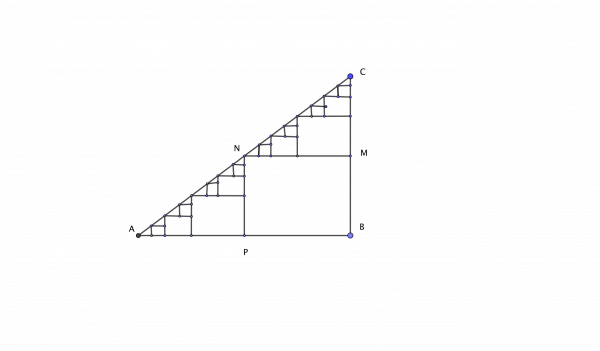
Considere um triângulo com catetos medindo 6 e 8 (veja figura abaixo). Qual será hipotenusa? Vamos considerar pontos médios de BC e AB chamando M e P. É fácil ver que se N for ponto médio de AC, então a escada CM-MN-NP-PA (união deste 4 segmentos) mede 6+8 = 14. Repetindo o mesmo argumento para triângulos CMN e NPA, vamos obter uma escada de 8 segmentos medindo 14 novamente. Seguimos este processo muito e sempre o comprimento da escada fica 14. Claro que a escada cada vez fica mais próximo à  hipotenusa, portanto o comprimento da hipotenusa é aproximadamente 14!!!!!! Verdade ou falso? por quê? 

Vamos voltar ao círculo e Archimedes. Homem que controlou o infinito e conseguiu encurralar o número $  \pi.$

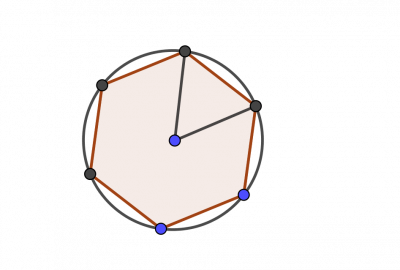
Considere um hexágono regular inscrito num círculo de raio r. Então o perímetro do hexágono é igual a  6r. Portanto $ P= 2\pi r > 6r$ e então $ \pi > 3$.

Claro que o grande Archimedes não parou por ai. Ele estimou o perímetro de círculo por baixo e por cima pelo perímetros de polígonos regulares circunscritos e inscritos.

Usando 96-gonos regulares ele logrou

$ 3 + 10/71 < \pi  < 3 + 10/70 = 22/7$

Não é extra-ordinário? Sabe como ele fez?  veja problema 38 no livro: 100 great Problems of Elementary Mathematics.

Na figura abaixo desenhamos 9-gono inscrito e circunscrito:

Sim, e este é um exemplo do limite, onde observamos que o limite é geralmente mais “bonito”. O que quer dizer isto? O lado esquerdo é uma soma de infinitos números!

9/10 + 9/100 + 9/1000 + …

é extremamente cansativo somar tantos números! De fato é impossível fazer isto, pois preciso de tempo infinito. Porém usando cálculo podemos somar N termos iniciais:

$ \sum_{i=1}^{N} 9/10^i = \frac{10^{N+1} -1}{10^N} - 9 = 1 - 1/10^N.$

Veja que a medida que escolhemos um N grande, o resultado da soma será muito perto de 1.

Será que para algum N, essa soma é igual a um? Não! nunca!

Tem outra soma que podemos adivinhar usando geometria euclidiana!

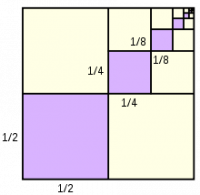
Olha para figura abaixo e tenta se convencer que $ 1/4 + 1/16 + \cdots 1/4^n + \cdots = 1/3$.