(Tolstoy?): Homem é como uma fração. O numerador é o que é de verdade e denominador o que ele pensa sobre si. Cada vez que o denominador aumenta, ele diminui.

test Números naturais são os que conhecemos desde primeiros anos de vida. Aprendemos números inteiros $ \mathbb{Z}$ cedo também. Em seguida aprendemos frações números racionais. Vale lembrar que os números racionais por muito tempo eram como os únicos números. A primeira descoberta de números irracionais é atribuida a Hipaso (um dos seguidores de Pitágoras) que infelizmente foi jogado ao mar pelos outros seguidores do Pitágoras por acreditar em números não racional!

Em vez de começar com argumento do Hipaso vamos apresentar o exemplo mais simples de um número irracional: A hipotenusa de um triângulo retangular com catetos iguais a 1 não pode ser racional, ou seja hipotenusa e catetos não são comensuráveis, i.e não existem $ m, n \in \mathbb{Z} , m \sqrt{2} = n $

De fato pode se mostrar que se n é um número natural e não é quadrado perfeito então $\sqrt{n}$ não é racional.

Veja https://pt.wikipedia.org/wiki/Algoritmo_de_Euclides para mais informações.

Dado dois números $ a_0 < a_1 $ queremos achar um outro número tal que ambos $a_0, a_1 $ sejam múltiplo inteiro deste último.

Seja $ n_1$ maior número inteiro tal que $ na_1 \leq a_0 .$ Assim

$ a_0 = n_1 a_1 + a_2, 0 \leq a_2 < a_1 $

Se $ a_2=0 $ então $ a_1 $ é o número que procurávamos. Caso contrário fazemos o mesmo processo com $ a_1 $ e $ a_2 $. Assim obtemos $ n_2 $ e $ a_3 $ tais que

$ a_1 = n_2 a_2+ a_3, 0 \leq a_3 < a_2 $

Se $ a_3=0 $ então $ a_2$ é o número desejado. (ambos $ a_0 $ e $ a_1$ são múltiplo de $ a_2 $). Caso contrário continuamos o processo. Se este processo parar, i.e

$ a_{k-1} = n_k a_k $

então $ a_k $ é o número desejado. Acontece que em alguns casos este processo não vai parar! assim dizemos que $ a_0 $ e $ a_1 $ não são comensuráveis. Veja o argumento de Hipaso a seguir.

Afirmação é que o lado de um pentâgono regular e seu diagonal não são comensuráveis.

$ a_0= $ comprimento de diagonal e $ a_1= $ comprimento do lado do pentâgono

Vamos usar seguintes fatos de geometria euclideana ($ABCDE$ e $A^{'}B^{'}C^{'}D^{'}E^{'}$ são respectivamente pentâgono maior e menor):

1. $ \frac{AB}{AC} = \frac{EB^{'}}{ED} $ usando semelhança de triângulos.
2. $ ABCB^{'} $ é um paralelogramo e portanto $ \frac{a_1}{a_0} = \frac{a_0 - a_1}{a_1} $. Denotamos por $ a_2 = a_0 - a_1.$ Observe, já que $a_1 < a_0$ então $ 0 < a_2 < a_1 $. Também é claro que $ a_0 = 1 \times a_1 + a_2 $
3. Temos que $ AD^{'}A^{'}C^{'} $ é paralelogramo e portanto o diagonal de pentágono menor $ A^{'}B^{'}C^{'}D^{'}E^{'} $ é $ a_2 $ e seu lado igual $ a_3= a_1 - a_2$ Argumentado como o caso do pentágono inicial, concluimos que $ a_1 = 1 \times a_2 + a_3, $ sendo que $ 0 < a_3 < a_2 $
4. continuando assim temos $ a_2 = 1 \times a_3 + a_4, 0 < a_4 < a_3 $ e $ a_3 = 1 \times a_4 + a_5 $ onde $ 0 < a_5 < a_4 .$
5. continuando este argumento e substituindo $ a_{n+1} = a_{n-1} - a_n $ teremos $ a_{n-1} = 1 \times a_n + a_{n+1} $

já que sempre $ a_n \neq 0 $ concluimos que $ \frac{a_0}{a_1} $ não é racional!

Essa última afirmação precisa de um argumento. Precisamos verificar que se dois números são comensuráveis, então o algoritmo de euclides é finito.

De fato:

A forma que representamos $ \frac{a_1}{a_0} $ é chamada de fração contínua. Hoje em dia, essa forma de representação não é usual para números. Entretanto frações contínuas formam parte de um tópico interessante para aproximar números irracionais.

Sejam $m, n$ dois números inteiros e vamos representar $\frac{m}{n}$ de forma decimal. Para isto dividimos $m$ por $n$. Se $n$ dividir o $m$, então não teremos resto na divisão e terminamos. Se não, teremos um resto na divisão de $m$ por $n$ que é menor do que $n$ e maior do que zero. multiplicamos este resto por 10 e novamente dividimos por $n$ e teremos novamente um resto…..se o processo parar, então:

$ m/n = c_0 + c_1/10 + c_2/100 + \cdots + c_k/10^k $ e representamos $ m/n = c_0,c_1c_2c_3\cdots c_k $. O processo pode não parar. Neste caso, já que sempre os restos pertencem aos números $ 0, 1, \cdots, n-1 $ então algum momento teremos repetição e portanto a sequência dos restos é uma sequência pré-períodica (i.e existe $ i_0 >0 $ e $ k < n $ tais que $ c_{i+k} = c_i $ para todo $ i > i_0 $ ). Assim realizamos que a representação decimal de qualquer número racional ou é finita ou pré-períodica.

Exemplo de um número racional (pré-períodico): $ 0,123454545454545454545..... $ ou $ 0,232323232323..... $ (períodico).

Seguindo este tipo de representação podemos chamar qualquer sequência $ c_0,c_1c_2c_3\cdots$ onde $ c_i \in \{0,1,...9\} $ como um número real e as sequências que não são pré-períodicas serão os números irracionais!

Exemplo de um número irracional:

Sem dúvida @s curios@s devem ficar embaraçad@s para saber por que o $x$ acima é um número!! O que é um número e $ 0,c_1c_2c_3,\cdots $ significa o quê? CALMA!

Não vamos se preocupar para responder o que é um número. (começou a primeira vez que tentamos ignorar certos rigores ….isto deve ocorrer com frequência e as vezes até faz bem, como vamos observar nos próximos capítulos).

Vamos entender por que a representação decimal realmente representa um número! O que significa $ c_0,c_1c_2\cdots ? $

Começamos com interpretação geométrica: Vamos fixar um segmento de reta como unidade e o comprimento de todos os possíveis segmentos formam todos os números reais positivos. Assim podemos considerar uma semi-reta (denotamos por $ R^+$) colocando uma das extremidades como 0 (grande invenção este tal de zero!) e assim todos os números podem ser representados como um ponto na semi-reta. Podemos definir relação <, usando a localização dos pontos na semi-reta.

$ [a,b] = \{x \in R^+ , a \leq x \leq b\} , a \leq b $

$ ]a,b[ = \{x \in R^+ , a < x < b\} , a < b $

$ [a,b[ = \{x \in R^+ , a \leq x < b\} , a < b $

$ ]a,b] = \{x \in R^+ , a < x \leq b\} , a < b $

Definimos um objeto monstruoso:

$ [a, \infty [ = \{ x , x \geq a\} $

Proposição: Sejam e, C dois números positivos. Então existem $ m, n $ naturais tais que

$ (1+e)^m > C$ & $ (1+e)^{-n} < C. $

Demonstração: Se expandirmos $ (1+e)^m = 1+me + $ (algo positivo) e pela propriedade Arquimediana existe m tal que $ me > C $ e portanto $ (1+e)^m > C. $ Tente mostrar a existência do n agora.

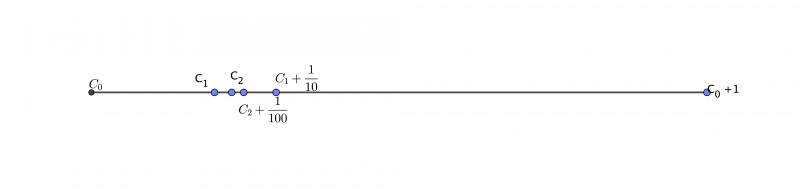
Dado um inteiro n, a expressão finita $ C_n = c_0,c_1,\cdots c_n $ faz sentido, não é?

Agora vamos observar que se aquele monstro $ c_0,c_1c_2\cdots $ for um número, ele deve ser maior de que $ C_n $. Ah, e tem que ser menor do que $ C_n + \frac{1}{10^n} $ (por quê? Pense!) Portanto conseguimos enjaular o monstro!! Seja qual for, está entre

$ C_n $ e $ C_n + \frac{1}{10^n} $. Pelos comentários acima observem que

$ C_0 \leq C_1 \leq C_2,... $ e $ C_0 +1 \geq C_1 + 1/10 \geq C_2 + 1/100 $

o seja teremos intervalos encaixados :  $ [C_i, C_i + \frac{1}{10^i}] $

A partir deste momento precisamos de um Axioma de completude (coisa que não se discute) e concluir que existe único número que está em todos os intervalos encaixados acima e assim achamos o monstro!

Observação : Se $ [a_n, b_n]$ é uma sequência de intervalos encaixados. Em princípio poderá haver mais do que um número que pertença a todos os intervalos. Tenta construir um exemplo.

====== Monstros Fake! (São mansos!)

Sabe quem é o monstro 0,999999…..? Ele é o velho amigo número inteiro 1.

pois, para todo n inteiro, usando soma das progressões aritméticas $ 0,9999...9 $ (n vezes o 9) $ = 1 - \frac{1}{10^n} $

$ 0,9999...9 $ (n vezes) $ \leq 0,99999.... \leq 0,9999...9 $ (n 9,s) $ + \frac{1}{10^n} = 1. $

o número 1 também satisfaz ambas as desigualdades acima e portanto pela unicidade (Axioma) teremos que o monstro é igual a 1.

Dado um conjunto dos números reais $ S $ dizemos que $ S $ é limitado superiormente se existir um número real M tal que $ M \geq x $ para todo $ x $ em $ S $.

Vamos a uma noção sofisticada chamada menor limite superior de um conjunto, ou supremo de um conjunto. Dado um conjunto $ S $, se $ S $ não for limitado então não tem supremo. Se for limitado então um número M é chamado de supremo se

$ S $ é limitado superiormente por M Para qualquer número real N, se $ S $ é limitado superiormente por N , então $ M \leq N. $

Axioma de completude (outra forma): Se um subconjunto é limitado superiormente então tem um supremo.

Exemplos: o supremo do conjunto $ [2,3[ $ é igual a 3. e o conjunto dos números inteiros não é limitado superiormente.

qual é o Supremo do conjunto $ \{x: x \in \mathbb{Q}, x^2 < 2 \} $?

ou supremo do conjunto $ \{\frac{(-1)^n}{n}, n \in \mathbb{Z}, n \neq 0 \} $.