Critério da segunda derivada: Seja $ f $ uma função definida num intervalo em torno de $ a $ e duas vezes diferenciável no ponto $ a $ e além disto $ f^{'}(a)=0 $ (ou seja $ a $ é um ponto crítico). Então:

Se $ f^{''}(a) > 0 $ então $ a $ é um ponto mínimo local, Se $ f^{''}(a) < 0 $ então $ a $ é um ponto máximo local.

Observação: Se “por azar” $ f^{''}(a) =0 $ não podemos afirmar nada a não ser que tenhamos alguma informação sobre outras derivadas. Vamos ver no final desta página.

Demonstração: Utilizamos polinômio de Taylor de segundo grau $ P_2(x) $ e sua propriedade fundamental:

$ \lim_{x \rightarrow a} \frac{f(x)-P_2(x)}{(x-a)^2} =0. $

Lembramos que (usando a hipótese $  f^{'}(a)=0. $):

$ P_2(x) = f(a) + (x-a)f^{'}(a) + \frac{1}{2} (x-a)^2  f^{''}(a) = f(a) + \frac{1}{2} (x-a)^2  f^{''}(a) $

Portanto concluímos que:

$ \lim_{x \rightarrow a } \frac{f(x)- f(a)}{(x-a)^2} - \frac{f^{''}(a)}{2} =0.  $

Sendo assim temos:

Se $ f^{''}(a) > 0 $ para todo $ x $ suficientemente próximo ao ponto $ a $          $ \frac{f(x)- f(a)}{(x-a)^2} >0  $ e portanto para tais $ x $ temos que $ f(x) > f(a). $ Isto significa que $ a $ é um mínimo local. Se $ f^{''}(a) < 0 $ para todo $ x $ suficientemente próximo ao ponto $ a $          $ \frac{f(x)- f(a)}{(x-a)^2} < 0  $ e portanto para tais $ x $ temos que $ f(x) < f(a). $ Isto significa que $ a $ é um máximo local.

Teorema: Seja $ I $ um intervalo e $ f: I \rightarrow \mathbb{R} $ duas vezes diferenciável e sua segunda derivada seja positiva (negativa) no intervalo $ I $. Então dado qualquer ponto $ a $ no interior de $ I $, então se $ x \neq a $ temos $ (x,f(x)) $ está acima (abaixo) do ponto $ (x, L(x)) $ onde $ L(x) $ é a ordenada do ponto na reta tangente ao gráfico da função no ponto $ a. $

No primeiro caso temos:

$ f(x) > f(a) + f^{'}(a)(x-a) $

e no segundo caso:

$ f(x) < f(a) + f^{'}(a)(x-a). $

O resultado acima dá uma informação sobre concavidade do gráfico da função no intervalo $ I. $ No caso segunda derivada positiva a função é chamada convexa (ou concavidade para cima) e se a segunda derivada for negativa a função é chamada de côncava (ou concavidade para baixo).

Demonstração:

Basta lembrar o teorema de valor médio adaptado:

$ f(x) - (f(a) + f^{'}(a)(x-a) = \frac{1}{2} f^{''}(c)(x-a)^2 $ para algum ponto entre $ a $ e $ x $.

Ponto de inflexão:

Seja $ a < b < c $ e o sinal da segunda derivada da função $ f $ no intervalo $ (a, b) $ seja oposto do sinal no intervalo $ (b, c) $ então o ponto $ b $ é chamado de ponto de inflexão.

Se a segunda derivada for uma função contínua, claro que $ f^{''}(b) =0. $

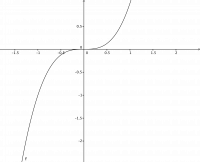
na figura abaixo o ponto $ x=0 $ é o ponto de inflexão da função cúbica $ f(x)=x^3. $ Observe que $ f^{''}(x)=6x $ que tem sinal oposto em torno do ponto $ x=0. $

Cuidado: 

Um ponto onde segunda derivada é zero não é necessáriamente ponto de inflexão. Por exemplo se $ f(x)=x^4 $ claramente $ f^{''}(0)=0 $ mas pelo fato de que $ f^{''}(x)=12x^2 $ não temos alteração do sinal da segunda derivada em torno do ponto $ x=0. $ (veja o gráfico para acreditar que não existe nenhuma inflexão!)

*

Teste de resistência! (Para curios@s)

Suponhamos que $ x=a $ é um ponto crítico e $ f^{''}(a)=0. $ Assim não podemos aplicar o teste da segunda derivada. Vamos olhar para terceira derivada se existir.

Se $ f^{'''}(a) >0 $ então podemos concluir que $ a $ não é um ponto máximo ou mínimo local.

$ f(x)= f(a) + \frac{(x-a)f^{'''}(a)}{3!} + Err(x) $ onde $ \frac{Err(x)}{(x-a)^3} \rightarrow 0 $ quando $ x \rightarrow a. $

portanto

$ \frac{f(x)-f(a)}{(x-a)^3} > 0 $ para $ x $ muito próximo de $ a. $

Analisando sinal do numerador e denominador concluímos que $ x=a $ não é mínimo, nem máximo.

***

suponhamos que a terceira derivada também se anular. Resistimos! olhamos para derivada de órdem quatro, $ f^{(4)}(a). $ Usando polinímio de grau quatro concluímos que:

se $ f^{(4)}(a) > 0  $ então $ a $ é mínimo local. se $ f^{(4)}(a) < 0  $ então $ a $ é máximo local.

e se a quarta derivada anular….

Teste de derivada de órdem k:

Seja $ f $ uma função $ k $ vezes diferenciável num ponto $ a $ no interior de seu domínio e que $ f^{(i)}(a)=0, i=1,2,.., k-1 $ e $ f^{(k)}(a) \neq 0. $ então:

Se $ k $ for par, dependendo se $ f^{(k)}(a) > 0 $ ou $ f^{(k)}(a) < 0 $, $ a $ é um mínimo local ou máximo local. se $ k $ for ímpar, então o ponto $ a $ não é nem máximo, nem mínimo local.