Na primeira aula falamos do método de exaustão do Arquimedes e a forma engenhosa que ele inventou para calcular área inscrita em algumas curvas. De fato historicamente o cálculo de áreas vem antes de calcular taxa de variação ou derivadas. Num curso de cálculo moderno, aprendemos as taxas de variação, antes de aprender como calcular áreas!

Para completar essas traições históricas, vamos definir função logaritmo usando noção de área de baixo do gráfico de uma função. De fato logaritmo foi introduzido por J. Napier e também Joost Burgi. O interesse e motivação deles era simplificar números grandes e seus produtos. Uma das propriedade importante do logaritmo (veja final desta página) é “transformar o produto em soma e progressões geométricas em progressões aritméticas”.

Para conhecer um pouco mais a história veja a página de Mathematical Association of America    (agradecemos Prof. Parham Salehyan por indicar essa página.)

Considere  $ f(t) = \frac{1}{t} $ como uma função de $ t > 0 $. O gráfico desta função é como a seguir :

Agora vamos definir outra função $ ln : (0, \infty) \rightarrow \mathbb{R} $:

$ ln(x) = $ área abaixo do gráfico da $ f $ entre $ 1 , x $ , se $ x \geq 1 $. No gráfico acima, referimos a área do “trapezoide curvi-linear” com vértices $ (1,0), (x, 0), (1,1), (x, \frac{1}{x})$.

Se $ x <1 $ definimos $ ln(x) = - ln(\frac{1}{x}). $

Alguns corolários da definição:

1. $ ln(1)=0 $
2. $ ln(x) $ é uma função estritamente crescente de $ x $.
3. $ ln $ é uma função contínua. Isto é um pouco mais delicado e precisa de alguma demonstração.

  A função $ ln: (0, \infty) \rightarrow  \mathbb{R} $ é uma função contínua em todo $ x \in (0, \infty) $.

Já que a definição desta função foi baseada numa intuição sobre área, a demonstração da continuidade também usará noção da área.

Seja primeiramente $ x \in (1, \infty) $ e escolhemos $ h $ pequeno para que $ x-h $ e $ x+h $ também pertençam ao intervalo $ (1, \infty) $.

No desenho abaixo $ A = (x, 0), B=(x+h, 0) $. A função $ f $ é estritamente decrescente e portanto pela figura (apenas visualizamos um pedaço do gráfico da $ f $), temos seguintes desigualdade entre áreas:

$ area(ABDF) < area(ABCD) = ln(x+h) - ln(x) < area(ABEC)    $

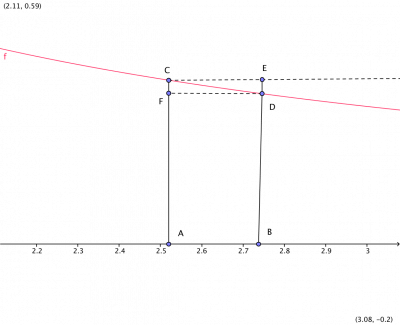Observe que área de retângulo $ ABDF $ é igual $ h \times f(x+h) = \frac{h}{x+h} $ e a área do retângulo $ ABEC $ é $ h \times f(x) = \frac{h}{x} $ ou seja  se $ h > 0 $:

$ \frac{-h}{x} < ln(x+h) - ln(x) < \frac{-h}{x+h}  $

Se $ h < 0 $ temos também:

$ \frac{h}{x} < ln(x) - ln(x+h) < \frac{h}{x+h}  $

e portanto em geral

$ \frac{|h|}{|x|} < |ln(x) - ln(x+h)| < \frac{|h|}{|x+h|}  $

Observe que quando $ h \rightarrow 0 $   os dois extremos das desigualdades acima tendem a zero e portanto pelo teorema de Sandwich temos que $ ln $ é uma função contínua.

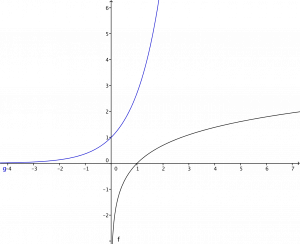
Vamos colocar o gráfico da função logaritmo (usando geogebra):

Calcule  $ \lim_{x \rightarrow 1} \frac{ln(x)}{x-1} $.

Observe que vamos enfrentar um limite “do tipo $ \frac{0}{0} $” .

Vamos usar as desigualdades que obtivemos anteriormente (comparação das áreas).

$ x > 1 \Rightarrow  \frac{x-1}{x} < ln(x) < (x-1)  \Rightarrow \frac{1}{x}  <  \frac{ln(x)}{x-1} < 1 $

Portanto usando a ideia do Teorema de Sandwich concluímos que

$ \lim_{x \rightarrow 1^+} \frac{ln(x)}{x-1}=1 $.

Vamos ver o que ocorre quando $ x \rightarrow 1^{-} $. Observe que

$ x< 1 \Rightarrow ln(x) = - ln(\frac{1}{x}) $ e

$ \frac{ln(x)}{x-1} = \frac{- ln(\frac{1}{x})}{- x( \frac{1}{x} -1)} $

Agora se chamarmos $ y = \frac{1}{x} $ então $ y \rightarrow 1^+ $ e portanto:

$ \lim_{x \rightarrow 1^-} \frac{ln(x)}{x-1} = \lim_{y \rightarrow 1^+}  \frac{y ln(y)}{y-1} =  1 \times 1 = 1 $.

Conclusão:

$ \lim_{x \rightarrow 1} \frac{ln(x)}{x-1} = 1 $.

Logaritmo “em outras bases”: As vezes consideramos outra função

$ \log_{10} : (0, \infty) \rightarrow \mathbb{R} ;\quad  \log_{10}(x) = ln(x) ln(10) $

Geralmente escrevemos $ \log_{10}^x $ em vez de $ \log_{10}(x) $.

Lembrando que a função $ ln: (0, \infty) \rightarrow \mathbb{R} $ é uma função injetiva e além disto é sobrejetora. Assim, podemos definir a função inversa

$ exp: \mathbb{R} \rightarrow \mathbb{R}$ cuja imagem é $ (0, \infty) $.

Já que a função exponencial é inversa da função logaritmo, podemos adivinhar como é seu gráfico. Ele é simétrico do gráfico da função $ ln $ com respeito do diagonal do plano (curva azul). Já que a função exponencial é inversa de uma função contínua, ela é contínua também.

Provavelmente, voce que está lendo essa página, deve saber que a função logaritmo tem uma propriedade mágica:

$ ln(ab) = ln(a)+ln(b) $. Por que será? 

Não é fácil neste momento demonstrar isto. Porém, já que é uma propriedade muito conhecida vamos tentar dar uma justificativa (que num certo sentido é uma prova, se adicionarmos um pouco mais de tempero de rigor!)

Para facilitar vamos considerar caso em que $ a, b \geq 1 $.

Na figura abaixo, vamos considerar $ a=2, b=3 $  apenas para ilustrar a ideia.

Observe que pela definição de $ ln(x) $, para mostrar $ ln(2\times 3) = ln(2) + ln(3) $.

$ ln(2 \times 3) $ é a área debaixo do gráfico de 1 até 6 que é a soma de dois números: área entre 1 até 2 + área de 2 até 6

Na figura abaixo analisamos a área abaixo do gráfico de 2 até 6 (região I). Afirmamos que essa área é igual a área abaixo do gráfico de 1 até 3 (região II).  Se provarmos essa afirmação concluímos que  $ ln(6) = ln(2) + ln(3) $.

Vamos cobrir cada região com segmentos verticais. Observe que podemos fazer uma correspondência entre segmentos da região I e região II. A cada segmento da região I baseado no ponto $ (t,0) $ , correspondemos um segmento na região II com comprimento dobro baseado no ponto $ (\frac{t}{2}, 0) $.

Região I

Região II

Agora um pulo de gato (não é um pulo dishonesto!): área da região I = área da região II

Para se convencer, lembre que se dobrarmos a largura de um retângulo, dividindo seu comprimento por 2, sua área não altera! De fato estamos usando mesmo tipo de argumento!

Bem, agora falta o(a) leitor(a) continuar o argumento para outros valores de $ a, b $.

Já que estamos convencid@s da propriedade básica $ ln(ab) = ln(a)  + ln(b) $ vamos usar a definição da função exponencial e concluímos (exercício) que

$ exp(x+y) = exp(x) exp(y) $

Essa propriedade é muito legal. Vamos brincar! Denotamos por $ e= exp(1) $

$ exp(2) = exp(1+1)=exp(1)exp(1)= e^2 $

continuando assim podemos verificar que $ exp(n)=e^n $

Em seguida podemos mostrar que para todo número racional $ exp(\frac{p}{q}) = e^{\frac{p}{q}} $.

Agora vamos usar o fato de que a função $ exp $ é contínua para definir potência irracional do número $ e $. Advinha como definir!!!!

$ e^{r} := exp(r) $  

Observe que em princípio não fazia sentido elevar um número a uma potência irracional (tipo $ \pi $ ). Porém temos direito de definir ela usando a função exponencial cujo domínio é o conjunto de todos os números reais.

Exercício: Calcule o seguinte limite:

$ \lim_{x \rightarrow 0} \frac{e^x -1}{x} $.

Alguns lugares no mundo onde encontramos logaritmo:

Magnitude de Terremotos: A famosa escala Richter para medir intensidade de terremotos é calculada usando logaritmo:

$ M = \log_{10}^A + B $  onde $ A $ é a amplitude (em mm) medida pelo sismográfi e $ B $ é um fator de correção de distância.

Pela definição e propriedade de logaritmo concluímos que um terremoto de magnitude 7 é 10 vezes mais intenso de que um terremoto de magnitude 6 na escala Richter.

Medir som: o volume de som é medido em decibels (dB):

$ v= 10 \log_{10}^{P \times 10^{12}} $

onde $ P $ é a pressão sonora.

Acidez (pH): A acidez é medida com pH e é calculada como a seguir:

$ pH = - \log_{10}^{[H^+]} $ onde $ [H^+] $ é a concentração molar do hidrogênio iônico dissolvido.