(texto adaptado do livro Infinite Power, Strogatz)
Vamos considerar a duração de cada dia do ano, medida em minutos desde nascer do sol ao pôr do sol. Fora do equador e equinócio (que ocorre duas vezes ao ano) os dias do ano tem duração variada. Os solstícios de inverno e verão podem ser definidos a partir dos dias mais curtos e mais longos, respectivamente. Os equinócios e solstícios demarcam o início das estações do ano (verão, outono, inverno e primavera).
Utilizamos o site (Date and Time info) para esboçar seguintes gráficos. Veja os dados captados neste arquivo.
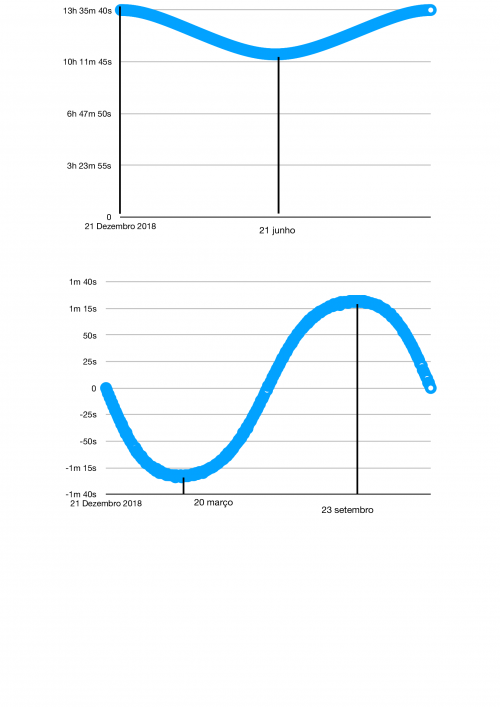
O primeiro gráfico representa a duração de cada dia desde 21 de dezembro de 2018 por um ano.
Como podemos observar 21 de dezembro que foi primeiro dia de verão teve maior duração (um dos máximos desta função) e que foi um dos solstícios. Outro solstício foi em 21 de junho que foi início do inverno.
Em outro gráfico esboçamos o crescimento da duração com respeito ao dia seguinte. Assim no dia 21 de dezembro que tivemos o dia mais longo, a duração do dia quase foi igual a do dia 22 de dezembro e a partir daí a duração caiu e a caída foi acentuada até o dia 20 de março que foi equinócio. Neste equinócio tivemos maior variação (negativa) da duração do dia. A partir daí o decaimento da duração dos dias foi menor até o dia 21 de junho onde tivemos segundo solstício.
O primeiro gráfico pode ser considerado como gráfico de uma função $ f $ e o segundo gráfico é da função $ g $
$ (*) g(x) = f(x+1) - f(x) = \frac{f(x+1)-f(x)}{(x+1)-x}.$
o gráfico da $ f $ é muito similar ao gráfico da função coseno (talvez com mudança de variável). Enquanto o segundo gráfico assemelha função $ -sen $ que é a derivada da função coseno! (veja abaixo. Derivada de funções trigonométricas)
Apesar de que os gráficos abaixo de fato são apenas um número fínito de pontos (e não realmente gráfico de uma função com domínio um intervalo) e na definição (*) acima não temos nenhum limite, o segundo gráfico parece como “derivada” do primeiro gráfico e isto deve ser considerado como uma evidência da potência de cálculo para entender natureza!
Derivada de funções trigonométricas
Vamos calcular a derivada de duas funções trigonométricas. Na próxima página vamos tratar outras funções.
Calculamos a derivada da função $ cos $. De fato vamos mostrar que $ cos^{'}(x) = -sen(x) $
$ cos^{'}(x) = \lim_{h \rightarrow 0} \frac{cos(x+h) - cos(x)}{h} = $
$ = \lim_{h \rightarrow 0} \frac{cos(x)cos(h) - sen(x)sen(h) - cos(x)}{h} $
$ = \lim_{h \rightarrow 0} \frac{cos(x)(cos(h)-1)}{h} - \lim_{h \rightarrow 0} \frac{-sen(x) sen(h)}{h} = -sen(x) $
No último passo utilizamos seguintes limites anteriormente calculados:
$ \lim_{h \rightarrow 0} \frac{sen(h)}{h} =1, \lim_{h \rightarrow 0} \frac{cos(h)-1}{h} = 0. $
Como um exercício mostrem que $ sen^{'}(x) = cos(x).$