Na aula anterior mostramos que $\lim_{x \rightarrow 0} \frac{1-cos(x)}{x^2} = \frac{1}{2}.$ Claro que todos adoramos os computadores e calculadoras maravilhosas. Porém veja:

• $\frac{1-cos(0,1)}{0,01} \sim 0,499583472197$
• $\frac{1-cos(0,01)}{0,0001} \sim 0,4999995833347$
• $\frac{1-cos(0,001)}{0,000001} \sim 0,499999958333$
• …

porém na aula (com um computador velinhos) a partir de um certo número de vezes a resposta era zero. Isto provavelmente $cos(0,00000\cdots 1)$ é quase igual a um e subtraindo de um, resulta zero e assim dividindo por $x^2= (0,00000\cdots)^2$ dá zero!

Na aula anterior também mostramos que o seguinte limite não existe:

$ \lim_{x \rightarrow 0} sen(\frac{1}{x}) $

Apesar do que o limite acima não existe, a função $ f(x) = sen(\frac{1}{x}) $ é limitada, $ |f(x)| \leq 1, x \in D(f). $ Usando este fato podemos concluir  seguinte:

$ \lim_{x \rightarrow 0} x sen(\frac{1}{x}) = 0. $

Vamos enunciar um resultado que em particular implica a afirmação acima.

Demonstracão: Seja $ \epsilon > 0 $  qualquer. Já que $ \lim_{x \rightarrow a} f(x) =0 $ concluímos que existe $ \delta> 0 $ tal que

se $ x \in S, 0 < |x-a|< \delta $ então $ |f(x) - 0| \leq \frac{\epsilon}{M}. $

Portanto $ |f(x)g(x)| \leq \frac{\epsilon}{M} \times M = \epsilon. $

Reflita um pouco na demonstração da proposição anterior. Observe a importância de número zero na hipótese $ \lim_{x \rightarrow a} f(x)=0.$ De fato se este último limite não fosse zero, não poderiamos concluir a tese da proposição. Dê um exemplo!

Tratando problemas concretos de aplicação do cálculo em alguns problemas de física ou engenharia, podemos encontrar funções que não tem limite porém possuem limites laterais!

Suponhamos que $ f: S \rightarrow \mathbb{R} $ uma função dada e $ a \in \mathbb{R} $ . Consideramos dois seguintes conjuntos:

1. $ S^{-} = \{ x \in S : x < a \}  $

2.  $ S^{+} = \{ x \in S : x >a\} $

Se $ a $ for um ponto limite de $ S^{-} $ (respectivamente $ S^{+} $) então podemos definir

$ \lim_{x \rightarrow a^{-}} f(x) $ ( respectivamente $ \lim_{x \rightarrow a^{+}} f(x) $  )

Exemplo:

Seja $ f(x) = [x]$ onde $ [x]$ representa a parte inteira do $ x$, i.e o maior número interio que é menor ou igual a $ x.$ Por exemplo $ [2,1] =2$ e $ [-2,1] = -3.$

Vamos caclular $ \lim_{x \rightarrow 0^+} f(x) $ e $ \lim_{x \rightarrow 0^-} f(x) $.

Observe que quando $ x < 0 $ está “próximo” a $ 0$ então $ f(x) = -1 $. Na verdade se $ -1 \leq x < 0  $   então $ f(x) = -1. $ Portanto

$ \lim_{x \rightarrow 0^-} f(x) = -1. $

Escrevendo rigorosamente:

Para todo $ \epsilon > 0 $ existe $ \delta > 0 $ tal que se

$ 0 < 0-x \leq \delta $ então  $ |f(x) - (-1)| \leq \epsilon $.

De fato dado qualquer $ \epsilon $ basta escolher $ \delta= \frac{1}{2} $.

Agora verifiquem que $ \lim_{x \rightarrow 0^+} f(x) = 0 $.

O que significa $ \lim_{x \rightarrow +\infty} f(x) ? $

Para falar do limite acima, estamos considerando $ + \infty $ como um “ponto limite” do domínio da função. De fato basta que exista uma sequência $ a_n \in D(f) $ tal que  $ \lim_{n \rightarrow \infty} a_n = + \infty $

Escrevemos  $ \lim_{x \rightarrow + \infty} f(x) = L $   se para qualquer $ \epsilon > 0 $ existe $ M $ tal que para qualquer $ x \geq M $ no domínio da função temos $ |f(x) - L| \leq \epsilon . $

Exercício: O que significa $ \lim_{x \rightarrow - \infty} f(x) = L $?

Exercício: Interpreta $ \lim_{x \rightarrow a^+} f(x) = - \infty . $

Exercício: Dê exemplo de uma função que $ \lim_{x \rightarrow - \infty} f(x) = + \infty $  (basta considerar $ f(x) = -x. ) $

Assíntota vertical: Dizemos que uma função tem assíntota vertical $ x=a $  se ocorrer pelo menos uma das seguintes condições:

$ \lim_{x \rightarrow a^+} = \pm \infty $ (o limite é infinito positivo ou infinito negativo) $ \lim_{x \rightarrow a^-} = \pm \infty $

Exemplo:

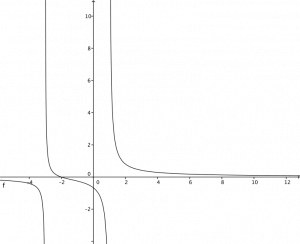
$ f(x) = \frac{x+2}{x^2+2x-3} $

observe que neste exemplo as raízes de denominadora da regra da função são $ 1, -3 $:

$ \lim_{x \rightarrow 1^-} f(x) = -\infty $ e

$ \lim_{x \rightarrow 1^+} f(x) = +\infty $

verifique os limites laterais em $ -3 $

Assíntota horizontal:

Dizemos que uma função tem assíntota horizontal $ y=a $ se ocorrer pelo menos uma das seguintes condições:

$ \lim_{x \rightarrow + \infty} f(x) = a $ $ \lim_{x \rightarrow - \infty} f(x) = a $

Vejam exemplo abaixo: $ f(x) = \frac{sen(x)}{x}  $. Podemos verificar que $ \lim_{x \rightarrow \infty} f(x) = 0 $ (ambos os limites no $ \pm \infty $ é igual a zero.)

Observe que a função não está definida no ponto $ x=0 $ porém já que

$ \lim_{x \rightarrow 0} f(x) = 1 $ podemos extender a função no zero (foi isto que geogebra fez quando esbocou o gráfico para mim!)

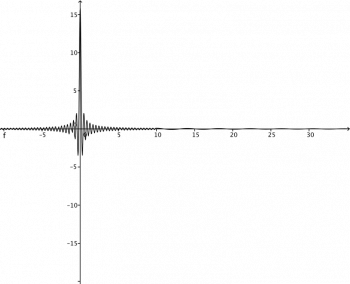
o exemplo a seguir quase é a mesma função: $ f(x) = \frac{sen(16x)}{x} $

Reflita um pouco sobre diferença e semelhança entre essas duas funções!

Assíntota oblíqua:

Dizemos que uma função tem assíntota oblíqua $   y = ax+b,   a \neq 0 $  se ocorrer pelo menos uma das seguintes condições:

$ \lim_{x \rightarrow + \infty} f(x) - (ax+b) = 0 $ $ \lim_{x \rightarrow - \infty} f(x) - (ax+b) = 0 $

Observe que se uma função possuir assíntota oblíquo então pelo menos uma das seguintes deve ocorrer:

$ \lim_{x \rightarrow + \infty} f(x) = + \infty $ $ \lim_{x \rightarrow + \infty} f(x) = - \infty $ $ \lim_{x \rightarrow - \infty} f(x) = + \infty $ $ \lim_{x \rightarrow - \infty} f(x) = - \infty $

Em seguida calculamos $ \lim_{x \rightarrow} \frac{f(x)}{x} = a $ e

$ b = \lim_{x \rightarrow \infty} f(x)-mx  $

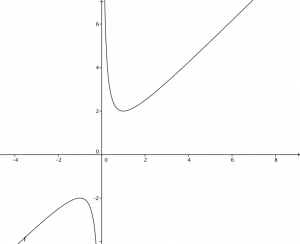
Exemplo : Considere $ f(x) = \frac{x^2 + 1}{x} $ e verifique que $ y=x $ é uma assíntota olblíqua.

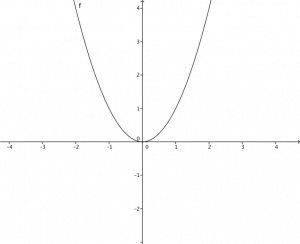
Non-example: verifiquem que a função $ f(x) = x^2 $ não tem nenhuma assíntora.  $ \lim_{x \rightarrow \infty f(x) = \infty} $, porém nenhuma reta pode beijar o gráfico desta função no infinito!

Exercício: Calcule seguintes limites, se existem.

$ \lim_{x \rightarrow 0^+} ( \frac{1}{x} - [ \frac{1}{x} ] ) $

$ \lim_{x \rightarrow 0^+} (1 - x [ \frac{1}{x} ]) $

$ \lim_{x \rightarrow 0^+} \frac{[x]}{x}$

O último limite acima esclarece por que as vezes falamos que escrever $ \frac{0}{0} $ é indecente! Observe que quando $ \lim_{x \rightarrow 0^+} [x] = 0 $ e $ \lim_{x \rightarrow 0^+} x =0 $. Certo?

Sim, porém a função de numerador não apenas tende ao zero. Ela é igual a zero, para $ 0 < x < 1 $. Portanto para tais valores de $ x $ temos $ \frac{[x]}{x} = 0 $ e concluímos que o limite desejado é zero.

Agora tenta analisar $ \lim_{x \rightarrow 0^-} \frac{[x]}{x} $.