De fato o estudo de limite de funções foi motivado por outro tema que é a DERIVADA de uma função. Suponhamos que um objeto está em queda livre. Não é difícil acreditar que a “velocidade” deste objeto varia ao longo do tempo. Logo surge a noção de velocidade instantânea.

Suponhamos que um objeto está na posição $d_0$ no momento $t_0.$ Se a posição dele no momento $t_1 > t_0$ for $d_1$, então definimos sua velocidade média neste intervalo de tempo como

$\frac{d_1- d_0}{t_1 - t_0}.$

Desde os tempo de Galileo, o celaculo de velocidades foi um problema intrigante. Apenas com descoberta do cálculo diferencial pelo Newton e Leibniz tivemos respostas rigorosas a pergunta de velocidade instantânea.

Seja $d : \mathbb{R} \rightarrow \mathbb{R}$ denotar a posição de uma partícula no momento $t$ na reta de números reais (para facilitar vamos assumir que $D(d) = \mathbb{R}$). Definimos a velocidade instantânea no momento $t \in \mathbb{R}$ como o limite das velocidades médias entre os tempos $t$ e $s$ quando $s$ convergir a $t.$ Ou seja,

$\lim_{s \rightarrow t} \frac{d(s) -d(t)}{s-t}.$

Pronto! estamos com um problema de cálculo de limite de funções. Fixamos $t$, Podemos definir uma função

$g(s) :=  \frac{d(s)-d(t)}{s-t}$,

e a velocidade instantânea será igual a $\lim_{s \rightarrow t} g(s).$

Lembrem (na definição do limite) que para definir limite acima, não precisamos que a função $g$ esteja definida no ponto $t$.

Exemplo 0: Calcule $\lim_{x \rightarrow 1} f(x)$ onde $f(x) = x-1.$

Neste casos, podemos advinhar logo o limite:

$\lim_{x \rightarrow 1} (x-1) = 0.$

Podemos demonstrar usando quantificadores: Para todo $\epsilon > 0$ existe $\delta > 0$ tal que se $0 < |x-1|\leq \delta$ então $|f(x)- 0| \leq \epsilon.$

Ora, $|f(x) - 0| = |x-1|$. Portanto basta escolher $\delta = \epsilon$ para garantir a desigualdade desejada.

Se queremos que $|f(x) - 0| \leq 0.09$ basta que $|x-1| \leq 0.09$.

Vamos agora a um exemplo não trivial:

Exemplo 1: Calcule $\lim_{x \rightarrow 0} \frac{sen(x)}{x}.$

Este limite é um dis limites fundamentais que vamos usar bastante no futuro. Porém neste momento precisamos refletir bem para perceber que “não é fácil” de advinhar! Para começar a função nem está definida no ponto $x =0.$ Observe também que não podemos usar ferramentas como última proposição da aula anteior:

o limite do denominador da função $\frac{sen(x)}{x}$ quando $x \rightarrow 0$ é igual a um!

Bom, o numerador também tem limite igual a zero queando $x$ tende a zero.

Exatamente aqui reside a beleza do cálculo, pois precisamos achar para que ponto a divisão de dois números que estão ficando muito próximo a zero, vai convergir, se é que converge!

Vamos colocar a mão na massa: Para $x \neq 0, |x| < \pi/2$

$sen(x) < x < tan(x)$ ,   se $x > 0$ (pense! Compare áreas de triângulos e setor do círuclo com ângulo $x$ na figura abaixo para concluir essa desigualdade.)  e

$tan(x) < x < sen(x)$,   se $x < 0.$ (veja a figura abaixo)

Portanto se $x\neq 0$ teremos

$1 < \frac{x}{sen(x)} < \frac{1}{cos(x)}.$

Pois bem. Na aula anterior, verificamos que  $cos(x)$ é uma função contínua de $x$ e portanto $\lim_{x \rightarrow 0} cos(x) = cos(0) = 1$. Então, $\lim_{x \rightarrow 0} \frac{1}{cos(x)} = 1.$

Já que o valor da função $\frac{x}{sen(x)}$ para todo $x$ (próximo a zero, aliás $|x| < \pi/2$ ) está entre duas funções (função constante 1 e $\frac{1}{cos(x)}$) cujos limites quando $x \rightarrow 0$ coincidem e é igual a um, concluímos que

$\lim_{x \rightarrow 0} \frac{x}{sen(x)} = 1.$ (peraí, como??? veja abaixo!)

Portanto agora usando a última proposição da aula anterior, concluímos que

$\lim_{x \rightarrow 0} \frac{sen(x)}{x} = 1.$

No cálculo do limite acima, usamos um fato simples que tem um nome “gostoso”:

Exemplo 2: Calcule o limite abaixo:

$\lim_{x \rightarrow 0} \frac{1-cos(x)}{x}$.

Observe que quando $x$ tende a zero, o numerador da fração acima, $1-cos(x)$ converge a $1 - cos(0) = 0$. Portanto falando de uma forma informal, para calcular este limite precisamos entender o comportamento de divisão de uma quantidade por outra, enquanto ambas convergem ao zero.

Vamos adiantar um segredo indecente mais correto: neste exemplo, o numerador converge ao zero de uma forma mais forte que o denominador! Vamos ver o que isto quer dizer matemáticamente:

Uma igualdade trigonométrica importante: 

Usando a igualdade acima temos: $\frac{1-cos(x)}{x} = \frac{2 sen^2(\frac{x}{2})}{x}  = (sen(\frac{x}{2})) \frac{sen(\frac{x}{2})}{\frac{x}{2}} .$

Toda manobra que fizemos, é para escrever a fração inicial como produto de duas funções e usar o item (2) da proposição (propriedades básicas).

  $\lim_{x \rightarrow 0} \frac{sen(x/2)}{x/2} = 1$. Observe que já temos mostrado que $\lim_{x \rightarrow 0}\frac{sen(x)}{x} = 0$ portanto trocando $x$ por $x/2$ ainda o limite é um.

$\lim_{x \rightarrow 0} sen(\frac{x}{2}) = 0$. Pois a função seno é contínua em zero.

Sendo assim,

$\lim_{x \rightarrow 0} \frac{1-cos(x)}{x} = 0 \times 1 = 0  .$

No processo de cálculo do limite acima, fizemos algumas operações algébricas, massageando a função, para poder desvendar aonde ela converge quando a variável $x$ tende ao zero.

De fato como sugerido por um aluno do ICMC observe que este tipo de erro pode te levar a lugares obscuros! Veja por exemplo $\lim_{x \rightarrow 0} \frac{1-cos(x)}{x^2} = \frac{1}{2}$ porém usando o “argumento errado” acima teriamos $\lim_{x \rightarrow 0} \frac{1-cos(x)}{x} = \lim_{x \rightarrow 0} \frac{1}{x^2} - \frac{1}{x^2} = 0.$ ***

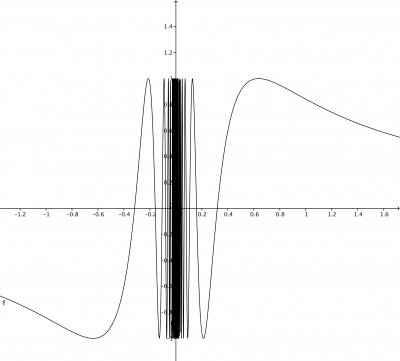
Exemplo 3: Verifique a existência de $\lim_{x \rightarrow} sen(\frac{1}{x}).$

Observe que $D(f) = \mathbb{R} \setminus \{0\}$ e portanto $x=0$ é um ponto limite do domínio da função. Portanto faz sentido perguntar sobre limite acima. Porém vamos ver que o limite não existe!

Um olhar intuitivo: Vamos olhar o gráfico desta função:

Bem, quando $x \rightarrow 0$ a função oscila muito! “A função não decide para qual valor convergir quando a variável $x$ tende ao zero.”

Vamos ver isto analiticamente: Suponhamos que exista algum limite $L$. Portanto para toda sequência $a_n \neq 0$ e que $a_n \rightarrow 0$ temos que ter

$\lim_{n \rightarrow} sen(\frac{1}{a_n}) = L.$

Agora, se escolhermos $a_n = \frac{1}{n \pi }$ concluímos que $L=0.$

Por outro lado se escolhermos $a_n = \frac{1}{n \pi + \frac{\pi}{2}}$ obteremos que $L = 1.$

Ora, mas pela definição se o limite existir, deve ser único número!