Gráfico de funções:

Para esboçar gráfico de uma função (quando não temos geogebra disponível!) vamos primeiramente averiguar o domínio da função.

Em seguida os pontos críticos e averiguar pontos máximo, mínimo, inflexão. Para tal, precisamos fazer uma tabelinha de sinal das derivadas. Se acharmos pontos da interseção com eixo $x$ (pode ser impossível ou difícil) e eixo $y$ podemos ter uma precisão melhor.

Finalmente, vamos procurar possíveis assíntotas horizontais, verticais e oblíquas da função.

Exemplos:

Seja $f: \mathbb{R} \rightarrow \mathbb{R}, f(x) = x^4 -x^3.$ Esboce o gráfico da $f.$

Claro que domínio da $f$ é toda reta real. Vamos calcular derivadas:

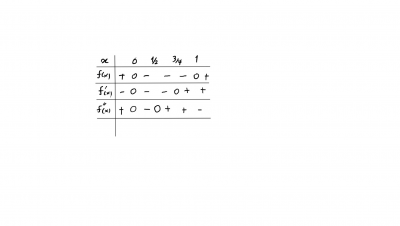
$f^{'}(x)=4x^3-3x^2, f^{''}(x)=12x^2-6x.$

Assim concluímos que $x=0, \frac{3}{4}$ são pontos críticos (onde a derivada se anula.) Pelo sinal da segunda derivada e teste da segunda derivada, o ponto $\frac{3}{4}$ é mínimo local. enquanto o ponto $x=0, \frac{1}{2}$ são pontos de inflexão.

É fácil ver que essa função não admite nenhuma assíntota.

Outro exemplo:

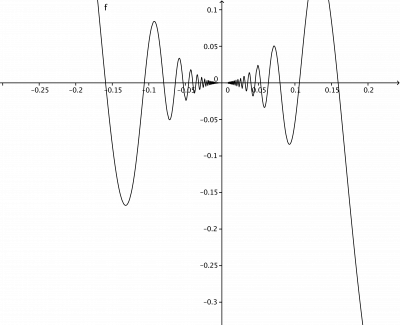
Esboce o gráfico da função $f$ dada pela equação $f(x)= x^2 sen(\frac{1}{x})$ se $x \neq 0$ e $f(0)=0.$ Ou seja a reta tangente no

ponto $x=0$ ao gráfico da função é horizontal.

Em todos os pontos exceto $x=0$ é fácil ver que a função é diferenciável. Verificaremos que no ponto $x=0$ também temos derivada. De fato anteriormente haviamos calculado $f^{'}(0)=0.$ Para todos  $x \neq 0$:

$f^{'}(x)= 2x sen(1/x) - cos(1/x)$

Para achar pontos críticos observe que se $f^{'}(x)=0$ então $tg(1/x)=\frac{1}{2x}.$

Afirmação: Existem $t_n \rightarrow \infty$ tais que $tg(t_n)= \frac{t_n}{2}, tg(-t_n)= \frac{-t_n}{2},$

Observe que isto implica que a  sequência $x_n = \frac{1}{t_n}$ converge a zero e $x_n, -x_n$ são pontos críticos.

Além disto, o sinal da derivada numa vizinhança pequena destes pontos altera:

$f^{'}(x)= (2xcos(1/x)) (tg(1/x) - \frac{1}{2x})$

em cada ponto $x_n$ o segundo fator é zero e muda de sinal numa vizinhança pequena e o primeiro fator não altera sinal.

Portanto os pontos $x_n$ são alternadamente pontos máximo e mínimo local.

Para ter uma precisão maior observe que $|sen(1/x)| \leq 1$ e portanto

$-x^2 \leq f(x) \leq x^2.$

A prova da afirmação:  Basta observar que o gráfico da função $t \rightarrow tg(t)$ e $t \rightarrow t/2$ se cruzam em infinitos pontos.

Exercício: Considere $f(x)= \frac{x}{2}+ x^2sen(1/x), x \neq 0$ e $f(0)=0.$ Mostre que $f^{'}(0) > 0$ porém em nenhum intervalo em torno do ponto $x=0$ a função não é crescente!

Lembrem que se num intervalo a derivada for positiva, então a função é crescente! Neste exemplo apenas verificamos a positividade da derivada no ponto zero.

Pode esbocar o gráfica da $f?$