(texto abaixo foi retirado do livro infinite powers, Strogatz)

A versão do cálculo diferencial do Fermat  é um excelente casamento entre álgebra e análise. Um dos problemas que ele considerou foi um simples adaptação de (hoje em dia) um exercício de otimização:

Imagine que você quer fabricar uma caixa com base  quadrada $x$ por $x$ e altura adequada para comprir regra de uma empresa aérea: A soma das medidas (altura, comprimento e largura) das caixas não podem ultrapassar 45 inchs. Quais serão as medidas da caixa para ter máximo de volume?

a intuição pode sugerir que um cubo é a melhor solução. De fato é! Porém vamos ver como o Fermat abordou este tipo de problema.

Primeiramente vamos utilizar símbolos algébricos (Primeiro texto usando álgebra para resolver problemas é pelo matemático Persa Al-Kharismi  cujo nome dá orígem a palavra algoritmo também): Denotando por $x$ o comprimento e largura e por $45-2x$ a alrtua, já que queremos volume máximo. Multiplicando as dimensões para obter volume, temos:

$V(x)= x^2 (45 -2x)= 45x^2 - 2x^3$

Qual é o valor do $x$ para que o volume, i,.e, $V(x)$ seja máximo?

Vamos esboçar o gráfico (usando geogebra)  da função $x \rightarrow V(x)$ para ter alguma ideia. ah, fiz uma contração na coordenada y para visualizar melhor. o gráfico abaixo é da função $x \rightarrow (45x^2-2x^3)/100$ que tem o mesmo valor x onde tem seu máximo.

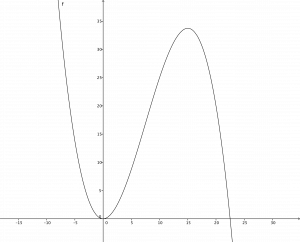“Dá para ver” que $x = 15$ é o ponto onde a função alcança seu valor máximo no problema desejado.  Ok, um(a) cientista não trabalho apenas com olhos. precisamos argumentar mais rigorosamente. Veja o que o Fermat fez, já que não tinha geogebra e outras tecnologias (inclusive a derivada, vejamos nas próximas páginas a noção de derivada):

Ele considerou a parte do gráfico da função entre $x=0$ e $x=22,5$ e observou que as retas horizontais abaixo de nível do máximo intersectam o gráfico em dois pontos enquanto retas acima deste nível não o cruzam. No valor máximo a reta horizontal “deve” intersectar o gráfico apenas em um ponto!

Então vamos botar a mão na massa! Quando a reta intersecta o gráfico em dois pontos $x=a, x=b$(lembrem que apenas estamos considerando $x \geq  0$) temos $V(a)=V(b)$ e portanto

$45a^2 - 2a^3 = 45b^2 -2b^3$

rearranjando a equação acima temos:

$45a^2 - 45b^2 = 2a^3 -2b^3$

agora com uma pitada de álgebra básica concluímos:

$45(a-b)(a+b) = 2(a-b)(a^2 + ab + b^2)$

Bem, vamos dividir os dois lados da equação por $a-b$. Podemos dividir? Sim, uma vez que $a \neq b$. Beleza! Teremos:

$45(a+b) = 2(a^2 + ab + b^2)$.

Agora vem o “pulo do gato Fermat”!  Neste momento, após de ter cancelado $a-b$ dos dois lados da equação, ele vem e coloca $a=b$ para achar o valor de tal ponto onde obteremos o máximo!

$45(2a) = 2(a^2 + a^2 + a^2)$ e portanto $90a = 6a^2$ e o valor aceito será 

$a=15$.

Mas será que o Fermat fez algo ilegal? humm

Não! De fato para $a$ muito próximo a $b$ teremos

$90a \sim 2(a^2+a^2+a^2)$. Em seguida, trocamos o símbolo de aproximação por igualdade! Ai, estmaos usando algum argumento de continuidade.