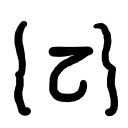Topologia e conjuntos em exercícios

1 Sejam $ \mathcal{M} $ e $ \mathcal{N} $ $ L $-modelos e $ h:M \to N $, são equivalentes: Solução

1. h é uma imersão (elementar).
2. Para toda fórmula atômica $ \varphi $ (para toda $ \varphi $) e toda valoração $ \alpha $ em $ M $, $ \mathcal{M} \models \varphi[\alpha] \iff \mathcal{N} \models \varphi[h \circ \alpha] $.

2 Seja $\mathcal{F}$ cadeia (cadeia elementar) de $L$-modelos:

2.1 Mostre que está bem definida $f^\mathcal{M}$

2.2 Para qualquer que seja $ \xi \in \kappa $, dada a cadeia (elementar) acima e $ \mathcal{M} = \bigcup \mathcal{F} $, $ \mathcal{M}_{\xi} \subseteq \mathcal{M} $ ($ \mathcal{M}_{\xi} \prec \mathcal{M} $).

Vamos assumir a linguagem $ L = \{\neg,\land,\to, \exists,=,\in, x_{0},\ldots\} $ com apenas um símbolo relacional não lógico, $ \in $, e variáveis.

Para evitar ambiguidade quando necessário, para diferenciar entre a linguagem do modelo e a meta-linguagem do universo em que estamos trabalhando, usemos $ \overset{\text{meta}}{=} $ e $ \overset{\text{meta}}{\in} $.

Note que estas são fórmulas onde todos os quantificadores estão ligados à uma variável que aparece relacionada por $ \in $ dentro da fórmula e que os termos são variáveis, visto que não existem funções e constantes na linguagem.

3 Vamos definir, por abreviação, a fórmula $ x \sim y $ por: \[ \forall z (( (z \in x )\to (z \in y)) \land ((z \in y) \to (z \in x))) \] 3.1 $ \mathcal{M} \doteq (M = \{a,\{a\},\{a,b\}\},\cdot^{\mathcal{M}}) $ e $ \mathcal{N} \doteq (N = \{a,b,\{a\},\{a,b\}\},\cdot^{\mathcal{N}}) $ são $L$-modelos na forma padrão.

1. Considere $ \alpha $ valoração com $ \alpha(x) = \{a\} $ e $ \alpha(y) = \{a,b\} $. Mostre que $ \mathcal{M} \models x \sim y [\alpha] $ mas $ \mathcal{N} $ não satisfaz a mesma proposição.
2. Conclua que $ x \sim y $ não é absoluta entre $ \mathcal{M} $ e $\mathcal{N} $.
3. Note que $ \mathcal{M} $ não sabe da existência de $ b $, e que apesar de $ \mathcal{M} \models x \sim y [\alpha] $, $ \alpha(x) \overset{\text{meta}}{\neq} \alpha (y) $.

3.2 Considere agora um $L$-modelo $ \mathcal{M}$ qualquer:

1. Mostre que $ \mathcal{M} \models x \sim y [\alpha] \iff $ $ \alpha(x)\cap M = \alpha(y)\cap M $.
2. Seja $ \mathcal{M} $ transitivo, mostre que $ \mathcal{M} \models (x \sim y) \iff \mathcal{M} \models (x = y) $.
3. Conclua que $ \mathcal{M} $ é transitivo, então $ \mathcal{M} \models \text{ extensionalidade} $.

4 Seja $\mathcal{M}$ um $L$-modelo e sejam $\phi,\psi$ $L$-fórmulas, podemos demontrar que:

4.1 $ \mathcal{M} \models \phi \lor \psi \iff \mathcal{M} \models \neg((\neg \phi)\land(\neg \psi)) $ e que $ \mathcal{M} \models \forall x \phi \iff \mathcal{M} \models \neg(\exists x (\neg \phi)) $. Pode-se demonstrar, analogamente, resultados parecidos para outros conectivos, definindo-os em termos de $\{ \neg,\land,\exists \}$.

4.2 Mostre que dada $ \phi $ existe fórmula $\psi$ construída usando-se apenas construções recursivas sob $\{ \neg,\land,\exists \} $ tal que $ \mathcal{M} \models \psi \leftrightarrow \phi $ usando indução sob a complexidade de $ \phi $.

4.3 Conclua que, ao fazer indução sob a complexidade de fórmulas, basta provar recorrendo sob as construções usando $\{ \neg,\land,\exists \} $.

5 Usando o 'atalho' fornecido pela questão anterior, vamos mostrar que seja $ \phi $ em $ \Delta_{0} $ e $ \mathcal{M},\mathcal{N} $ $ L $-modelos transitivos, então $ \phi $ é absoluta entre eles.

5.1 Começando das atômicas, $ \psi $ do tipo $ t = s $ são na verdade do tipo $ x = y $ igualdade de variáveis. O outro caso é $ x \in y $. Em ambos, temos que as atômicas são absolutas entre os modelos.Solução

5.2 Mostre sob recursão em $ \neg $ e $ \land $.Solução

5.3 Seja $ \phi $ absoluta entre os modelos, mostre que ainda o é a fórmula $ \exists x \in t \phi $.Solução

6 Mostre que existem fórmulas em $ \Delta_{0} $ equivalentes às (abreviações):

1. $ x = \emptyset $.
2. $ x \subset y $.
3. $ x=y $.
4. $ x = \{y,z\} $.
5. $ x = (y,z) $.
6. $ x $ é ordinal.
7. $ x = y \times z $.
8. $ x = \omega $.
9. $ x = dom(y) $.

obs.: note que se encontrarmos um modelo transitivo para uma fórmula $\Delta_0$, temos que qualquer modelo transitivo satisfaz tal fórmula.

7 Determine o rank de $\emptyset$, $\{\emptyset\}$, $\{\emptyset, \{\emptyset\}\}$, $\omega$ e $\omega \cup \{\omega\}$.

8 De fato, tem-se que:

1. $ V_{\alpha} $ transitivo.
2. $ V_{\alpha} \subset V_{\beta} $ se $ \alpha \leq \beta $.
3. $ X \subset V_{\alpha} $ e $ \alpha < \beta $ então $ X \in V_{\beta} $.
4. $ X \in V_{\alpha} $ então $ X \subset V_{\beta} $ para algum $ \beta < \alpha $.
5. $ X $ é um conjunto, $ rank(X) = \alpha $ $ \iff $ $( X \subset V_{\alpha} $ e $ \beta < \alpha \implies X \not \subset V_{\beta}) $.

9 Considere $ \mathcal{M} = (V_{\omega + \omega},\cdot^{\mathcal{M}}) $ modelo na forma padrão. Queremos mostrar, ao menos parcialmente, que $ \mathcal{M} \models ZFC\backslash\{\text{substituição}\} $.

9.1 Mostremos que $ \mathcal{M} \models ZFC \backslash \{\text{substituição}\} $.

1. Note que $ V_{\omega + \omega} $ é transitivo, logo, em particular ele modela extensionalidade. De fato, qualquer $ \Delta_0 $ para a qual existe modelo transitivo é satisfeita por $ \mathcal{M} $.
2. Prove que $ \mathcal{M} \models \{\text{união}\}$.Solução
3. Prove que $ \mathcal{M} \models \{\text{partes}\}$.Solução
4. Mostre para os outros axiomas.

9.2 Prove que $ \mathcal{M} \models \neg\text{substituição} $.Solução

9.3 Note que isso demonstra que o axioma da substituição é independente do restante de $ZFC$, assumindo que $ZFC$ é consistente.

10 Mostre que $ V_\omega \models ZFC \backslash \{\text{infinito}\} $.

11 Este é um roteiro para mostrar que todo conjunto admite um fecho transitivo. Seja $X$ um conjunto.

11.1 Defina $T_0 = X$ e $T_{n + 1} = \bigcup T_n$ para cada $n \in \omega$. Considere $tr(X) = \bigcup_{n \in \omega} T_n$. Note que $tr(X)$ é um conjunto tal que $X \subset tr(X)$.

11.2 Mostre que $tr(X)$ é transitivo.

11.3 Seja $Y$ transitivo tal que $X \subset Y$. Mostre que $tr(X) \subset Y$.

12 Esse é um roteiro para motivar a definição acima.

12.1 Dê um exemplo de um conjunto finito mas cujo fecho transitivo não seja finito.

12.2 Mostre que a coleção de todos os conjuntos unitários não forma um conjunto.

13 $ H(\kappa) $ é transitivo.Solução

14 Seja $ x $ um conjunto tal que $ rank(x) = \alpha $, então $ \{rank(y) : y \in tr(x)\} = \alpha $.Solução

15 Observe que, a priori, $H(\kappa)$ não é necessariamente um conjunto. Queremos demonstrar que este é o caso:

15.1 Dado $ \kappa $ infinito, seja $ x \in H(\kappa) $ então $ |tr(x)| < \kappa $, note que $ \{rank(y) : y \in tr(x)\} = \alpha = rank(x) $ está 'enumerado' por itens de $ tr(x) $ e portanto temos que $ |rank(x)| \leq |tr(x)| < \kappa $ .

15.2 Nesse caso, é possível mostrar que $ x \in V_\kappa $. Conclua que $ H(\kappa) $ é conjunto.

16 Mostre que $ H(\omega) = V_\omega $.Solução

17 Seja $ \kappa $ regular. Seja $ x \subset H(\kappa) $ tal que $ |x| < \kappa $, queremos mostrar que $ x \in H(\kappa) $. Se $\kappa = \omega$, temos o resultado.

17.1 Tome $\omega < \kappa $ regular e $ x $ como na hipótese, seja $|tr(x)| \geq \kappa$. Seja $ x_{0} = x $ tem $ |x_{0}| < \kappa $. Tome $ x_{n+1} = \bigcup x_{n} $, deve haver $ n $ o menor com $ |x_{n}| \geq \kappa $. Se $ |x_{n-1}| < \kappa$ e $ |\bigcup x_{n-1}| \geq \kappa $, note que encontramos $x_{n-1}\in tr(x)$ com $|tr(x_{n-1})| \geq \kappa $, mas havíamos assumido $x \subset H(\kappa)$.

17.2 Seja $ |tr(x)| = |\bigcup_{n \in \omega}x_n| = \sup \{|x_{n}| : n \in \omega \}= \alpha \geq \kappa $, note que também $\alpha \leq \kappa $. Mas então $\alpha = \kappa$, mas daí $ cf(\kappa) = \omega $.

18 Seja $ \phi $ uma fórmula do tipo função tal que $ a \in H(\kappa) $ então $ \phi(a) \in H(\kappa) $. Então dado $ A \in H(\kappa) $ temos que $ \{\phi(a) : a \in A\} \in H(\kappa) $.Solução

obs.: existe $ x \in H(\kappa) $, $ 2^{|x|} \geq \kappa $.

Fosse $ \kappa $ regular com $ \forall \alpha < \kappa \,\, 2^{\alpha} < \kappa $ ( que não $ \omega $). $ H(\kappa) = V_{\kappa} $ seria modelo para $ ZFC $.

Concluímos que $ \kappa $ não enum. regular então $ H(\kappa) $ é modelo para $ ZFC $ exceto pelo axioma das partes. Se é, $ \kappa $ é inacessível.