Existemiitas sequências “famosas”. Aqui apenas vamos mencionar algumas.

Exemplo : O Galileo queria compreender o movimento dos objetos. Dado que não havia relógios precisos, dificilmente poderia analisar o movimento de um objeto em queda livre. Nosso gênio tentou analisar o movimento de uma bola nas rampas lisa de inclinações variadas. E aha! Ele imaginou o movimento “vertical” como limite dos movimento nas rampas inclinadas. Ele usava relógio aquático para comparar tempos percorridos. A descoberta dele nas suas palavras: “A proporção das distância percorridas, nos tempos iguais, por um objeto deslizando (iniciando de repouso), é igual a proporção de números ímpares.” Ou seja se na primeira unidade de tempo, o objeto percorreu 1 unidade de distância, na segunda unidade de tempo percorrerá 3 unidade de distância,…e em linguagem de sequências teremos a sequência $a_n = 2n-1$

Observar a sequência de números ímpares em natureza forneceu um prazer enorme ao Galileo.

Vamos somar os termos da sequência $a_n$. Assim vamos obter uma nova sequência $b_1 = a_1, b_2 = a_1 + a+2 , b_3 = a_1+a_2+a_3, \cdots$

ou seja $b_n = a_1+a+2+\cdots a_n = \sum_{i=1}^{n} a_i$

Essa nova sequência revela a distância total percorrida após n unidades do tempo. E assim surge segunda sequência famosa $b_n = n^2$. Essa sequência é quadrática.

Veja a figura abaixo e tenta visualizar, por que $b_n = n^2.$

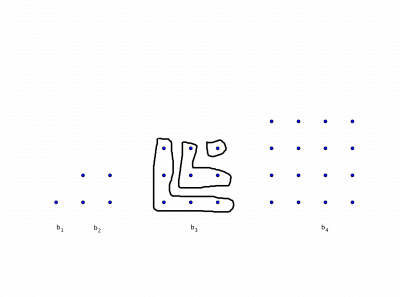Claro que haverá outras sequências famosas como cúbicas,… Em geral $a_n = n^k$

é uma sequência famosa que cresce com $n$ e seu crescimento é chamado de polinomial.

Sequência exponencial (A lenda do imperador e inventor de xadrez):

De acordo com a história, o jogo de xadrez foi inventado no século VI d.C por um homem muito inteligente. Ele viajou até Pataliputra para apresentar sua criação ao imperador. (Pataliputra é onde atualmente está localizada a cidade de Patna, na Índia Oriental.) O imperador ofereceu um prêmio ao inventor.

A contraproposta do inventor:

Como a bondade do imperador estava exacerbada por conta da criação, o inventor sugeriu que usassem o tabuleiro para determinar a quantidade de arroz que receberia. Propôs o inventor:

Sua Majestade, peço que coloque um único grão de arroz no primeiro quadrado do tabuleiro, dois no segundo, quatro no terceiro e assim por diante, para que cada quadrado receba o dobro de grãos de arroz que recebeu o anterior.

O imperador, impressionado com a aparente modéstia do inventor, garantiu o pedido e aceitou. Mas percebeu rápido que estava com um problema sério:

“ Após 32 quadrados, já havia dado ao inventor cerca de 4 bilhões de grãos de arroz. ”

A sequência correspondente é chamado de uma sequência exponencial

$c_n = 2^n$.

Comparando com sequência $b_n = n^2$ ambas as sequências $b_n, c_n$ crescem na medida que $n$ cresce. Porém existe uma diferença fundamental na maneira que cada uma delas cresce! $c_n$ cresce muito mais rápido do que $b_n$, aliás muito mais rápido que qualquer sequência polinomial. Como podemos provar isto?

Pensando no seu bolso, vamos poupar dinheiro e estudar uma sequência super famosa que pela primeira vez foi estudada por razões econômicas (dizem as lendas).

Suponhamos que voce ganhou 1 milhão de dolares por resolver um dos problemas de Clay institute e quer poupar num banco. O gerente do banco oferece taxa de jutos anual de d porcentos. Sendo assim seu saldo após um ano será de $1 + \frac{d}{100}$. Para faciliar denotamos por $r = \frac{d}{100}.$ Portanto seu saldo no final do ano será de $s_1= 1+r$ milhões.

Pensando um pouco, você vai negociar com seu gerente de seguinte forma: Eu deixo meu saldo no seu banco, se receber o juro de $\frac{d}{2}$ porcentos após 6 meses, prometendo que vai deixar seu dinheiro por um ano. O gerente que não havia estudado bem o cálculo 1, aceita a proposta.

Sendo assim seu saldo no final de um ano será de

$s_2 = (1 + \frac{r}{2}) (1 + \frac{r}{2})$ milhões!

Fazendo a conta você verifica que $s_2 = 1 + r + \frac{r^2}{4} > 1+r = s_1$. Obá! que tal fazer outra proposta:

Vamos calcular o juro composto a cada 4 meses …ou que tal a cada mês um juro de $\frac{d}{12}$ porcentos? O gerente que não havia estudado cálculo 1, aceita numa boa. você calcula seu saldo final do ano que será de

$s_{12} = (1+ \frac{r}{12})^{12}.$

Sabe como calcular $s_{12}?$ Bem,

$(1+ \frac{r}{12})^{12} = 1 + 12 \frac{r}{12} + \binom{12}{2} \frac{r^2}{144} + \cdots (\frac{r}{12})^{12} =$

$1 + r + \frac{11}{24}r^2 + \cdots > 1 + r + \frac{r^2}{4}.$

Maravilha! Isto é legal. que tal continuarmos assim e ganhar uma quantidade enorme de dinheiro? Será que podemos ganhar mais do que qualquer número desejado, apenas dividingo o ano em n períodos iguais e fazer juro composto de taxa $\frac{d}{n}$ porcentos?

$s_n = (1+\frac{r}{n})^n$. Essa sequência quando $n \rightarrow \infty$ tende a um número chamado de constante de Euler!

$\lim_{n \rightarrow \infty} (1+\frac{r}{n})^n = e^r$

onde $e \sim 2,7182818284590452353602874...$ é um constante famoso de Neper. Não vamos detalhar por que este limite existe. Num futuro próximo vamos analisar melhor. Porém já podemos demonstrar algo interessante:

Para ver isto, lembre que $(1+\frac{1}{n})^n= 1 + {n\choose 1} \frac{1}{n} + \cdots + {n \choose k} \frac{1}{n^k} + \cdots + {n \choose n}\frac{1}{n^n},$

onde ${n\choose k} = \frac{n(n-1)(n-2)\cdots (n-k+1)}{k!}.$

Agora observe que para $2 \leq k \leq n$ temos: $\cdots + {n \choose k} \frac{1}{n^k} = \frac{1}{k!} (1-\frac{1}{n})(1-\frac{2}{n})\cdots (1- \frac{k-1}{n}) < \frac{1}{2.3..\cdots k} < \frac{1}{2^{k-1}}$ e portanto:

$(1+\frac{1}{n})^n < 1+1+\frac{1}{2} + \cdots + \frac{1}{2^{n-1}} < 1+ \frac{1}{1-\frac{1}{2}} =3.$

Exercício: Considere uma sequância $a_n = \sqrt[n]{n}$. mostre que essa sequência é decrescente, isto é:

Após algumas aulas vai poder verificar para qual número essa sequência “vai convergir”! Tem algum chute?