Apresentação

Este trabalho faz parte do programa da disciplina de Introdução à Inteligência Artificial, do Programa de Mestrado e Doutorado em Ciência da Computação, do Instituto de Ciências Matemáticas e de Computação, da Universidade São Paulo, como parte dos requisitos de avaliação da disciplina, que está sendo ministrada neste primeiro semestre de 1999 pela Profa. Dra. Sandra Maria Aluísio.

Voltar ao Início

Objetivos

Permitir o aprendizado da linguagem de programação Prolog
Aplicar os conceitos de programação baseada em lógica
Aplicar os conceitos sobre listas, operadores, funções de E/S
Aplicar técnicas de "busca heurística" para manipulação de árvores de busca
Construir e aplicar funções "heurísticas" para otimizar o processo de busca
Aplicar o algoritmo Best-First Greedy na implementação da solução de um problema, conforme ilustra a Figura 01
Resolver um problema didático relatado na literatura de Inteligência Artifical

Figura 01 - Descrição, em pseudo-código, do Algoritmo Greedy Best First

Voltar ao Início

Problema

Este trabalho objetiva apresentar uma solução para o Problema da Criptografia Aritmética - CriptoArithmetic. Tal problema é um exemplo didático clássico da literatura de Inteligência Artificial, e consiste em gerar dígitos numéricos que transformem uma para uma seqüência de caracteres original em uma seqüência de caracteres criptografados. De modo geral, pode-se observar que a geração de dígitos passa pela definição de funções regras (heurísticas) que condicionem a análise e conversão dos caracteres de uma seqüência. Neste ponto, dois caracteres iguais devem receber o mesmo dígito, enquanto caracteres diferentes devem receber dígitos diferentes, conforme ilustra a Figura 02.

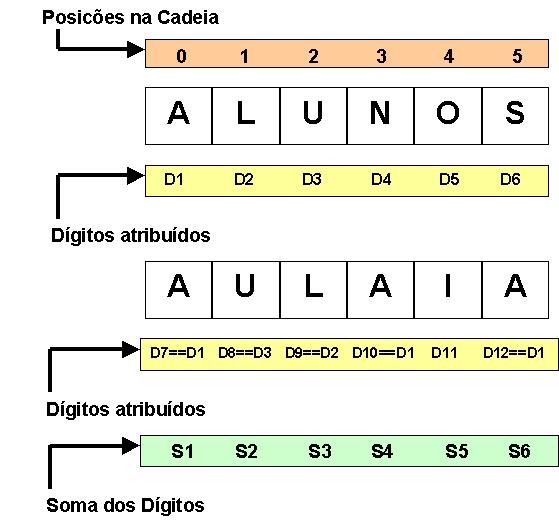
Figura 02 - Restrições para geração de dígitos

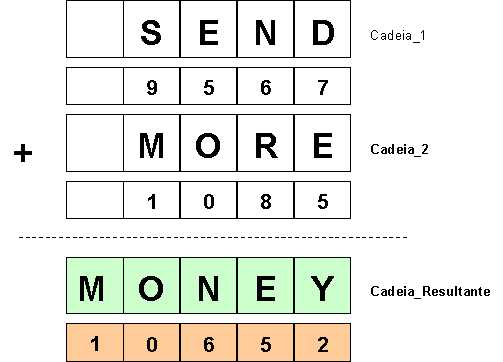
Figura 03 - Uma possível solução para a geração de dígitos

Voltar ao Início

Código-Fonte

O programa para resolver o problema da Criptografia Aritmética foi implementado na linguagem de programação PROLOG, e alguns trechos de código-fonte encontram-se descritos a seguir.

soma(N1, N2, N) :- % numeros representados como listas de digitos
soma1(N1, N2, N,
0, 0, % valores que são transportados da direita para a esquerda
[0,1,2,3,4,5,6,7,8,9], _). % todos os dígitos disponíveis para criptografia

soma1([], [], [], 0, 0, Digitos, Digitos).

soma1([D1|N1], [D2|N2], [D|N], C1, C, LISTADIGITOS1, DIGITOSGERADOS):-
soma1(N1, N2, N, C1, C2, LISTADIGITOS1, LISTADIGITOS2),
digitossoma(D1, D2, C2, D, C, LISTADIGITOS2, DIGITOSGERADOS).

digitossoma(D1, D2, C1, D, C, LISTADIGITOS1, DIGITOSGERADOS):-
apaga(D1, LISTADIGITOS1, LISTADIGITOS2),
apaga(D2, LISTADIGITOS2, LISTADIGITOS3),
apaga(D, LISTADIGITOS3, DIGITOSGERADOS),
S is D1 + D2 + C1,
D is S mod 10,
C is S divu 10.

apaga(A,L,L):-
nonvar(A), !. % uma variável ja instanciada

apaga(A,[A|L],L). % apaga a cabeça da lista

apaga(A,[B|L],[B|L1]) :-
apaga(A,L,L1). % apaga toda a cauda da lista

criptografia(1):-
soma1([D,O,N,A,L,D],
[G,E,R,A,L,D],
[R,O,B,E,R,T],
0,0, [0,1,2,3,4,5,6,7,8,9],_),
write('+-+-+-+-+-+-+'),nl,
write('|D|O|N|A|L|D| <-- Cadeia 1'),nl,
write(|),write(D),write(|),write(O),
write(|),write(N),write(|),write(A),
write('|'),write(L),write('|'),write(D),write('|<-- Digitos 1'),nl,
write('+-+-+-+-+-+-+'),nl,
write('|G|E|R|A|L|D| <-- Cadeia 2'),nl,
write(|),write(G),write(|),write(E),
write(|),write(R),write(|),write(A),
write('|'),write(L),write('|'),write(D),write('|<-- Digitos 2'),nl,
write('+-+-+-+-+-+-+'),nl,
write('|R|O|B|E|R|T| <-- Cadeia Resultante'),nl,
write(|),write(R),write(|),write(O),
write(|),write(B),write(|),write(E),
write('|'),write(R),write('|'),write(T),write('|<-- Digitos Resultantes'),nl,
write('+-+-+-+-+-+-+'),
nl.

Clique aqui para obter o código-fonte

Voltar ao Início

Resolução

Revisitando o problema da Criptografia Aritmética pode-se observar o alguns pontos relevantes. Inicialmente, cada símbolo ou letra é representado por apenas um dígito na resolução do problema. Em adição, para que uma letra possa ser trocada por um dígito, o resultado da expressão aritmética de cálculo do algoritmo deve estar correto. Neste ponto, o algoritmo utilizado pelo trabalho aqui reportado, manipula dígitos na base decimal; por tal motivo, as expressões aritméticas fazem uso de cálculos com o resto da divisão por 10 ( mod), e também com divisão por 10 ( divu).

Conforme mostra o código-fonte, um conjunto de recursos da linguagem Prolog foi utilizado para prover a solução do problema. Inicialmente, observa-se a manipulação de listas para armazenar os dígitos válidos para geração da criptografia, bem como listas para armazenar os dígitos que serão gerados pelo processo de criptografia.

Recursos de formatação de saída foram utilizados para gerar uma representação gráfica das cadeias de caracteres e dígitos correspondentes a cada caractere.

Predicados recursivos foram implementados para permitir a "busca heurística", através do algoritmo Greedy Best First, na lista de dígitos válidos e gerar as listas que contém a solução para o problema. Observa-se, ainda, a presença do predicado nonvar que verifica se um elemento de uma lista é uma variável e possui um valor instanciado.

Por fim, considerando-se o algoritmo Greedy Best First, pode-se observar as seguintes estratégias para resolução do problema:
- inicialmente, uma lista é construída para armazenar os dígitos válidos para o processo de criptografia;
- o predicado recursivo soma tem a função de instanciar valores que possam conduzir a um dígito válido para uma letra ou símbolo;
- o predicado recursivo soma1 gera um dígito para uma letra ou símbolo, a partir da avaliação da função heurística definida para o algoritmo;
- o predicado digitosoma avalia se um dígito gerado pode ser inserido na lista de dígitos válidos gerados para as letras anteriores;
- os predicados puzzle instanciam valores às listas, passando cadeias de caracteres que deverão ser avaliadas pelo algoritmo;
- os predicados criptografia1, criptografia2 e criptografia3 acionam a chamada do predicado soma que, recursivamente, gera as listas de dígitos que definem a solução para o problema.



Voltar ao Início

Casos de Teste

Considerando-se a implementação feita, os seguintes casos de teste foram realizados:
criptografia(1).
criptografia(2).
criptografia(3).
criptografia(4).


Como resultado do acionamento do motor de inferência da linguagem Prolog, obteve-se os resultados apresentados pelas Figuras 04, 05, 06 e 07.

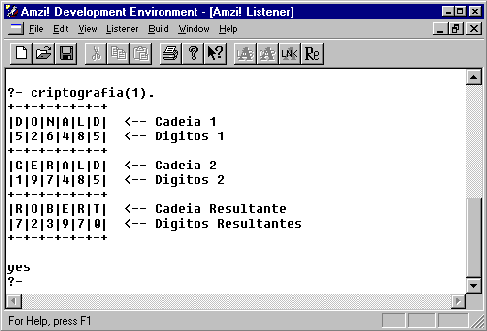
Figura 04 - Interface que ilustra o resultado do primeiro caso de teste do programa


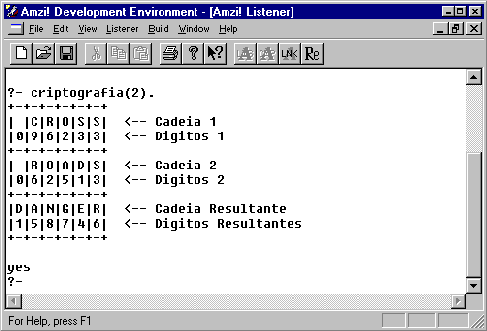
Figura 05 - Interface que ilustra o resultado do segundo caso de teste do programa


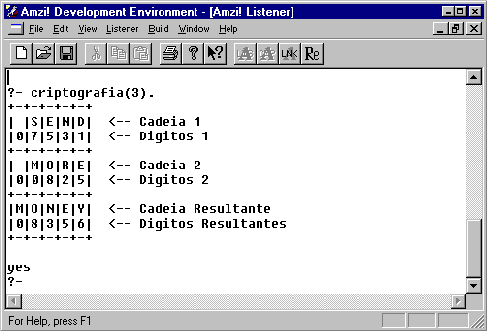
Figura 06 - Interface que ilustra o resultado do terceiro caso de teste do programa


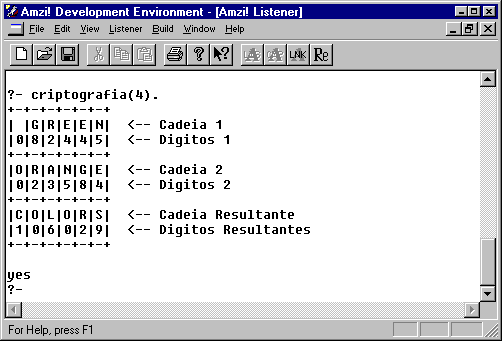
Figura 07 - Interface que ilustra o resultado do quarto caso de teste do programa

Voltar ao Início

Ambiente Prolog

Para o desenvolvimento do trabalho foi utilizado o Amzi Logic Explorer - Ambiente Integrado de Desenvolvimento obtido via download e instalado nos laboratórios do ICMC-USP.

Figura 08 - Ambiente Prolog utilizado para o desenvolvimento do trabalho Voltar ao Início


Conclusões

O trabalho aqui reportado contribuiu, inicialmente, para que os autores pudessem dar continuidade ao aprendizado da linguagem de programação Prolog, aprendizado este estimulado pelas aulas desta disciplina.

Em adição, ao implementar uma solução para o problema da Criptografia Aritmética, os autores puderam avaliar o algoritmo Best-First Greedy, em termos de busca com heurísticas, o que permitiu a consolidação dos aspectos teóricos apresentados em aula.

Por fim, a estratégia implementada apresenta boa eficiência por conseguir evitar situações de busca que conduzam a combinações de dígitos não-aceitáveis em relação às regras (heurísticas) definidas.

Voltar ao Início

Referências

ALUÍSIO, S.M.: Introdução ao Prolog. Notas de Aula da disciplina de Introdução à Inteligência Artificial. ICMC-USP, 1999.
BRATKO, I.: PROLOG: Programming for Articial Intelligence. Addison-Wesley Publishing, 1986.
MONARD, M.C. et al.: Introdução à Programação Prolog. Disponível on-line em http://www.labic.icmc.sc.usp.br, 1998.

Voltar ao Início