Grafos Planares
Algumas definições e alguns resultados das listas de conexidade e de árvores serão utilizados.
Dizemos que um grafo $G = (V,A)$ é um grafo planar se ele pode ser desenhado no plano de modo que suas arestas não se intersectam. Tal desenho será designado representação planar do grafo.
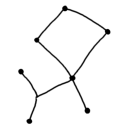
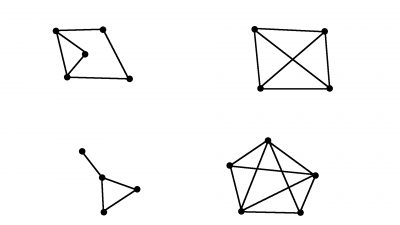
1 Todos os grafos conexos a seguir são planares. Desenhe suas representações planares.
2 Mostre que um subgrafo de um grafo planar é um grafo planar.
3 Mostre que toda árvore com uma quantidade finita de vértices é planar.
Em uma representação planar de um grafo planar, uma região ou face do grafo consiste em um conjunto maximal de pontos no plano tal que, dados dois desses pontos, existe uma curva ligando-os sem cruzar com arestas ou vértices do grafo.
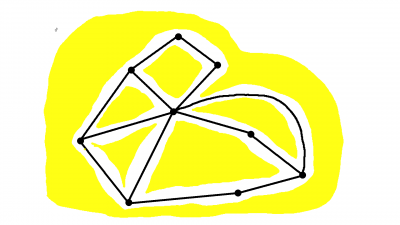
No grafo conexo planar abaixo, as regiões consistem nas áreas amarelas. Observe que há uma região que é ilimitada, sendo designada oceano do grafo.
4 Seja $G = (V,A)$ um grafo planar e $\{R_1,R_2,\dots,R_n\}$ o conjunto de suas regiões em uma representação planar. Denote por $b(R_i)$ a quantidade de arestas que delimitam a região $R_i$. Argumente por que $\displaystyle \sum_{i=1}^nb(R_i) \leq 2|A|$. A igualdade sempre vale?
5 Seja $G$ um grafo planar com uma quantidade finita de vértices. Mostre que $G$ é bipartido se, e somente se, $b(R)$ é par para toda região $R$ de uma representação planar desse grafo.
6 Seja $G$ um grafo conexo planar finito com $n$ vértices, $q$ arestas e $r$ regiões. Esse é um roteiro para verificar a fórmula de Euler, isto é, $n-q+r=2$.
6.1 Mostre que, se $G$ é uma árvore, a fórmula é verdadeira. Observe que, se $q=0$, $G$ é uma árvore.
6.2 Por indução, suponha que a fórmula é verdadeira se o grafo possui menos de $q$ arestas. Podemos considerar o caso em que $G$ possui um circuito. Verifique que a fórmula de Euler é válida nessa situação.
6.3 Conclua que o número de regiões de um grafo planar independe de sua representação planar.
7 Seja $G = (V,A)$ um grafo planar conexo com uma quantidade finita de vértices. Se $|V|\geq 3$ e $|A|\geq 3$, observe que cada região é delimitada por pelo menos três arestas. Conclua que $|A|\leq 3|V|-6$.
7.1 Mostre que $K_5$ não é um grafo planar.
7.2 Mostre que, se $G$ é um grafo planar conexo com menos de $12$ vértices, então $\delta(G) \leq 4$.
7.3 Mostre que, se $G$ é um grafo planar conexo, então $\delta(G)\leq 5$
8 Seja $G = (V,A)$ um grafo planar que não possui circuitos de três vértices como subgrafo. Se $V$ é finito, mostre que $|A|\leq 2|V|-4$.
8.1 Se $G$ é um grafo planar bipartido conexo, conclua que $\delta(G)\leq 3$.
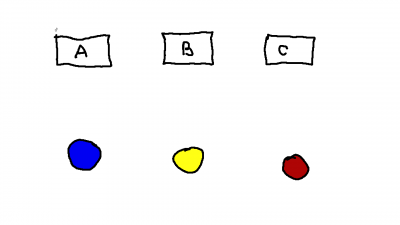
O problema abaixo é um quebra-cabeças clássico da matemática recreativa, conhecido como o problema dos três serviços.
9 Abaixo temos a representação de três casas (A, B e C) que devem receber os abastecimentos de água (azul), eletricidade (amarelo) e gás (vermelho) através de canos conectando cada casa aos serviços necessários. É possível fazer essa conexão sem que haja cabos se cruzando?
O grafo que representa as conexões a serem feitas no problema dos três serviços é conhecido como $K_{3,3}$. Nessa lista, vimos que esse grafo, juntamente com o $K_5$, não é planar. Na realidade, em 1930, Kuratowski percebeu que todos os grafos não planares possuem $K_{3,3}$ ou $K_5$ como um tipo específico de subgrafo.