Grafos Bipartidos
Algumas definições e alguns resultados das listas de conexidade e de árvores serão utilizados.
Dizemos que um grafo $G = (V,A)$ é um grafo bipartido se existirem $V_1,V_2\subset V$ tais que $V = V_1 \cup V_2$, $V_1\cap V_2 = \emptyset$ e, dada $\{a,b\}\in A$ uma aresta, tem-se que $a\in V_1$ e $b \in V_2$ ou $b\in V_1$ e $a \in V_2$. Nesse caso, $\{V_1,V_2\}$ é chamada bipartição de $G$.
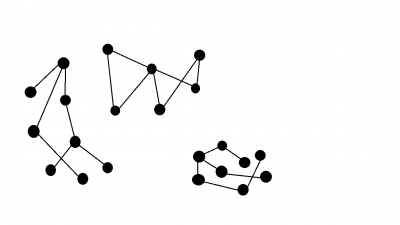
1 Observe o grafo cujo conjunto de vértices corresponde aos pontos pretos abaixo e cujas arestas estão todas representadas. Esse grafo é bipartido? Alguma de suas componentes conexas corresponde a um grafo bipartido? Se sim, quantas?
2 Mostre que todo caminho é um grafo bipartido. Todo circuito é um grafo bipartido?
2.1 Seja $G = (V,A)$ um grafo bipartido conexo. Mostre que ele admite uma única bipartição, isto é, se $\{V_1,V_2\}$ e $\{V_1',V_2'\}$ são bipartições de $G$, então $V_1 = V_1'$ (e, consequentemente, $V_2 = V_2'$) ou $V_1 = V_2'$ (e, consequentemente, $V_2 = V_1'$).
3 Seja $G = (V,A)$ um grafo bipartido finito em que todos os vértices possuem o mesmo grau. Mostre que, se $\{V_1,V_2\}$ é uma de suas bipartições, então $|V_1| = |V_2|$.
4 Seja $G = (V,A)$ um grafo bipartido finito. Mostre que $\delta(G)+\Delta(G)\leq |V|$.
5 Mostre que um grafo bipartido não possui um circuito com número ímpar de vértices como subgrafo.
5.1 Mostre que toda árvore é um grafo bipartido.
5.2 Mostre que, se um grafo não possui um circuito com número ímpar de vértices como subgrafo, então esse grafo é bipartido.
Com o exercício acima, mostramos que um grafo é bipartido se, e somente se, não possui circuitos ímpares.
6 Seja $G = (V,A)$ um grafo conexo e fixe $a\in V$. Mostre que $G$ é bipartido se, e somente se, $d(a,b) \neq d(a,c)$ para toda aresta $\{b,c\}\in A$.