Rato no Tabuleiro

betovs@icmc.sc.usp.br

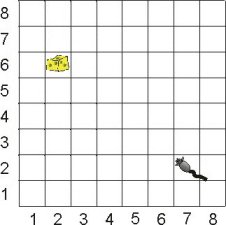
Um rato em uma posição de um tabuleiro de xadrez (Xr, Yr) quer pegar um pedaço de queijo em uma outra posição do tabuleiro (Xq,Yq). O rato lembra por onde caminha e não passa duas vezes pela mesma posição. Estando em uma posição ele pode se movimentar no máximo a qualquer das 8 posições vizinhas (não pode sair do tabuleiro). Determinar o caminho para pegar o queijo.

Acima temos ilustrado uma situação inicial do problema. O queijo se encontra na posição 2/6 do tabuleiro e o rato na posição 7/2. O rato pode se mover nas seguintes direções:

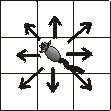
Estas direções serão representadas pelos 8 pontos cardinais n, s, l, o, no, ne, so, se. O mapeamento destes movimentos pode ser representado em prolog por:

A solução deste problema foi alcançada utilizando o algoritmo de busca A* que combina uma função heurística admissível h(n) com uma função de custo g(n), de maneira que sua função de avaliação é f(n) = h(n) + g(n).

A função de custo adotada para este problema foi a profundidade do nó na árvore de busca e a função heurística o número de passos necessários para alcançar as coordenadas do queijo. A função heurística pode ser expressada como:

onde, Xn/Yn representam as coordenadas do nó n no tabuleiro e Xq/Yq representam as coordenadas do queijo no tabuleiro.

Para não repetir um caminho já percorrido, as coordenadas percorridas são armazenadas em uma lista auxiliar durante a busca, assim quando os nós filhos de um nó são expandidos, os que possuem coordenadas já visitadas, não são inseridos na lista de nós a serem visitados.

A listagem mouse.pl contém o código com a solução deste problema.

Um sliding block puzzle, onde dada a configuração inicial :

deve-se obter:

Os movimentos são restritos a deslizar os blocos para o espaço em branco, ou trocar o espaço em branco com um dos seus blocos vizinhos. Estes movimentos foram representados em prolog como:

A solução deste problema foi alcançada utilizando o algoritmo de busca A* que combina uma função heurística admissível h(n) com uma função de custo g(n), de maneira que sua função de avaliação é f(n) = h(n) + g(n).

A função de custo adotada para este problema foi a profundidade do nó na árvore de busca. A função heurística é a combinação de dois estimadores freqüentemente utilizados em problemas de sliding blocks: a função de distância Manhattan, que calcula uma distância próxima até a solução, e a uma função fora-de-ciclo que penaliza o custo quando o estado está muito diferente do objetivo.

A solução deste problema está implementado em tryme.pl.

Vale lembrar que a execução deste algoritmo consome alguns minutos.