Hill-Climbing Problema das 8-rainhas

O objetivo do problema é colocar 8 rainhas em um tabuleiro de forma que nenhuma rainha ataque outra. (Uma rainha ataca outra se esta estiver na diagonal e/ou horizontal e/ou vertical). Este tipo de problema, pertence a classe dos casos em que dado um estado inicial a solução consiste em encontrar uma melhor configuração final, mesmo que esta não seja a mais satisfatória. Exemplificando, dado um estado inicial. As Figuras 1 e 2 mostram uma possível configuração inicial e final do tabuleiro.
 

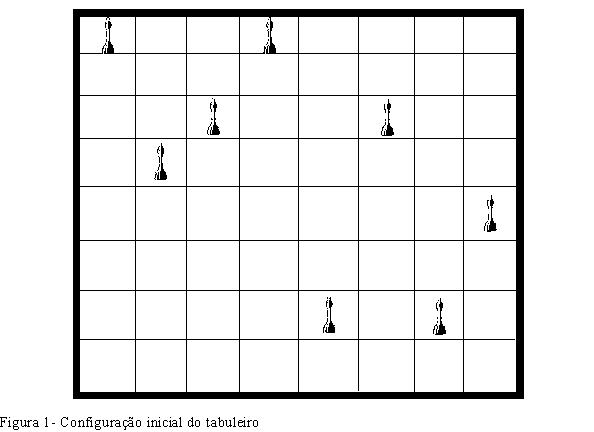
Uma solução satisfatória poderia ser:

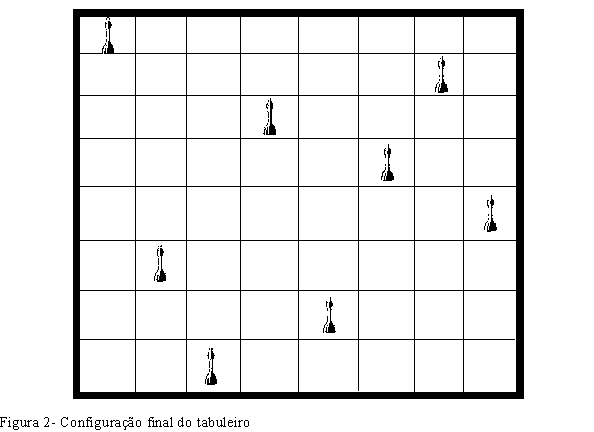
Descrição da resolução:

Foram desenvolvidas duas versões para o problema, as quais diferem basicamente pela forma de movimentação das peças no tabuleiro:

• Versão 1: movimenta uma rainha qualquer da sua posição original para uma nova posição cuja coluna não contenha outra rainha;
• Vantagens:
• é mais genérico pois permite que seja dada qualquer configuração inicial das rainhas no tabuleiro;
• encontra alguma solução para qualquer estado inicial;
• Desvantagens:
• maior custo computacional pois é mais complexo;
• a execução é um mais lenta que a outra versão;
• implementação mais complexa que a outra versão;
• gera mais estados na fase de expansão de um nó, consumindo grande quantidade de memória (pilha);
• Versão 2: movimenta uma rainha para uma outra posição na mesma coluna

• Vantagens:
• menor custo computacional pois é mais restrito;
• a execução é mais rápida;
• implementação mais simples;
• gera menos estados na fase de expansão de um nó, consumindo menos quantidade de memória (pilha) do que a versão anterior;
• Desvantagens:
• exige que a configuração inicial seja específica (deve ser colocada uma rainha em cada coluna);
• não encontra resposta satisfatória para casos que a configuração inicial não é a esperada.

Para a resolução do problema foram criados duas versões, estas se diferenciam por alguns aspectos:

• As configurações inicias (ou os estados iniciais) e
• a forma de movimentação das rainhas no tabuleiro.

• Estado
• Representação - lista de pares ordenados que representam as posições de cada rainha no tabuleiro;
• Versão 1: arranjo de 8 rainhas no tabuleiro de modo aleatório. Por exemplo: [(L1,C1),(L2,C2),(L3,C3),(L4,C4),(L5,C5),(L6,C6),(L7,C7),(L8,C8)];
• Versão 2: arranjo de 8 rainhas no tabuleiro, uma em cada coluna. Por exemplo: [(L1,1),(L2,2),(L3,3),(L4,4),(L5,5),(L6,6),(L7,7),(L8,8)];

• Estado inicial
• Múltiplos estados: qualquer estado permitido, em cada versão;

• Estado final
• Múltiplos estados: qualquer estado permitido que possui a característica de não haver ataque entre as rainhas;

operador

• O operador mover / 3 retorna a heurística referente ao novo estado;
• Versão 1: mover(Estado0, Estado1, Heurística);

% Dado um estado Est0, retorna em Est1 um estado correspondente a movimentação de uma rainha

% a partir do estado Est0

mover(Est0, Est1, H) :-

        permitido(R),
        not(elem(R, Est0)),
        troca(R1, R, Est0, Est1),
        coluna_diferente(R, Est1),
        heuristica_2(Est1, H).

% Permite a troca de posicao de dois elementos em uma lista
troca(R1, R2, [R1| Resto], [R2| Resto]).
troca(R1, R2, [R3| Resto1], [R3| Resto2]) :-
        troca(R1, R2, Resto1, Resto2).

% Determina a area permitida para a movimentacao das pecas (tamanho do tabuleiro)
permitido((L, C)) :-
        entre(L, 1, 8),
        entre(C, 1, 8).

% Determina se uma rainha esta em uma coluna diferente de todas as demais
coluna_diferente((L, C), []).
coluna_diferente((L, C), [(L, C)|Outras]):-
        !,
        coluna_diferente((L, C), Outras).
        coluna_diferente((L, C), [(L1, C1)|Outras]):-
        C \= C1,
        coluna_diferente((L, C), Outras).

% Predicado que verifica se um valor esta entre dois outros, permitindo instanciar
% este valor caso ele nao esteja instanciado
entre(_, Min, Max) :-
        Min > Max,
        !,
        fail.
        entre(X, X, _).
entre(X, Min, Max) :-
        ProxMin is Min + 1,
        entre(X, ProxMin, Max).

% Verifica se exite um elemento em uma lista
elem(X, [X| _]).
elem(X, [_| Xs]) :-
        elem(X, Xs).

• Versão 2: mover(Estado1, Estado2, Heurística);
% Permite a troca de posicao de dois elementos em uma lista

troca(R1, R2, [R1| Resto], [R2| Resto]).
troca(R1, R2, [R3| Resto1], [R3| Resto2]) :-
        troca(R1, R2, Resto1, Resto2).

% Dado um estado Est0, retorna em Est1 um estado correspondente a movimentação de uma rainha
% a partir do estado Est0
mover(Est0, Est1, H) :-
    entre(NovaLinha, 1, 8),
    troca((L, C), (NovaLinha, C), Est0, Est1),
    L \= NovaLinha,
    heuristica_1(Est1, H).

% Predicado que verifica se um valor esta entre dois outros, permitindo instanciar
% este valor caso ele nao esteja instanciado
entre(_, Min, Max) :-
    Min > Max,
    !,
    fail.
entre(X, X, _).
entre(X, Min, Max) :-
    ProxMin is Min + 1,
    entre(X, ProxMin, Max).

• Custo do caminho
• Zero, uma vez que o tipo de solução é o estado meta.

O algoritmo Hill-Climbing é classificado como Algoritmo de Melhorias Iterativas, e é utilizado para a resolução de problemas, cuja descrição do estado contém toda a informação necessária para a solução, ou seja, o caminho até a solução é irrelevante. É interessante notar também que este algoritmo mantém somente um estado (o mais promissor) na memória.

Devido as características acima a solução encontrada nem sempre é a solução ótima, uma vez que o algoritmo pode encontrar um máximo (ou mínimo) local, encerrando a busca.

O código a seguir exibe a implementação do algoritmo Hill-Climbing utilizado.

% Implementa busca informada - Algoritmo Hill Climbing

hill(I, F):-
    heuristica_1(I, H1),
    findall((H, Est), (mover(I, Est, H), H < H1), Lista_Est),
    minimo_lista1(Lista_Est, (H2, ProxEst)),
    H1 > H2,
    !,
    hill(ProxEst, F).
hill(I, I).

% Retorna o estado que tem a menor heuristica
minimo_lista1([L|Lc], Min):-
    min_l1(Lc, L, Min).

% Complemento do predicado minimo_lista1
min_l1([], Min, Min).
min_l1([L|Lc], MinAtual, Min):-
    maior1(L, MinAtual),
    !,
    min_l1(Lc, MinAtual, Min).
min_l1([L|Lc], MinAtual, Min):-
    min_l1(Lc, L, Min).

% Verifica qual heuristica eh maior
maior1((H, _), (H1, _)):-
    H > H1.

heuristica_1(Estado, Heuristica): a partir de um estado, esta heurística irá fornecer o número de rainhas que atacam uma (ou mais) rainha(s). Por exemplo: no estado representado na figura1 a heurística é 8, pois todas as rainhas atacam.

 

% Heuristica_1: retorna o numero de rainhas que atacam

heuristica_1(Est, H):-
    quantasAtacam(Est, Est, 0, H).

% Conta o numero de rainhas que atacam alguma outra rainha
quantasAtacam([], _, N, N).
quantasAtacam([R|Outras], Est, Ac, N):-
    ataca(R, Est, D),
    Ac1 is Ac + D,
    quantasAtacam(Outras, Est, Ac1, N).

% Determina se uma rainha ataca (1) ou nao (0)
ataca(R, Est, 0):-
    nao_ataca(R, Est),
    !.
    ataca(_, _, 1).

% Verifica se uma rainha nao ataca todas as outras do tabuleiro
nao_ataca(_,[]).
nao_ataca(R, [R|Outras]):-
    !,
    nao_ataca(R, Outras).
nao_ataca((L,C),[(L1,C1)|Outras]):-
    L \= L1,
    C \= C1,
    T is C1-C,
    T2 is L1-L,
    T \= T2,
    T3 is L-L1,
    T \= T3,
    nao_ataca((L,C),Outras).

heuristica_2(Estado, Heuristica): a partir de um estado, esta heurística irá fornecer o número total de ataques entre as rainhas. Por exemplo: no estado representado na figura1 a heurística é 22 ataques, no total, entre as rainhas.

 

% Heuristica_2: retorna o total de ataques entre todas as rainhas

heuristica_2(Est, H):-
    contaAtaques(Est, Est, 0, H).

% Conta o total de ataques entre todas as rainhas
contaAtaques([], _, N, N).
contaAtaques([R|Outras], Est, Ac, N):-
    conta(R, Est, 0, D),
    !,
    Ac1 is Ac + D,
    contaAtaques(Outras, Est, Ac1, N).

conta(_, [], N, N).
conta(R, [R1|Outras], Ac, N):-
    ((R \= R1, ataca1(R, R1), Ac1 is Ac + 1); Ac1 is Ac),
    !,
    conta(R, Outras, Ac1, N).

ataca1((L,C),(L1,C1)):-
    L = L1.
ataca1((L,C),(L1,C1)):-
    C = C1.
ataca1((L,C),(L1,C1)):-
    T is C1-C,
    ((T2 is L1-L, T = T2);
    (T3 is L-L1, T = T3)).

Heurística 1 X Heurística 2

A heurística 1 efetua uma contagem do número de rainhas que atacam alguma outra rainha. Isto é feito da seguinte maneira: para cada rainha R de um dado estado é feita uma busca neste estado até que seja encontrada uma outra rainha que seja atacada pela rainha R. Se nesta busca foi encontrada uma rainha atacada incrementa-se o número de rainhas que atacam (rainha R ataca alguma outra rainha).

A heurístcia 2 efetua uma contagem do número total de ataques entre todas as rainhas. Isto é feito da seguinte maneira: para cada rainha R de um dado estado é feita uma contagem do número de outras rainhas que ela ataca. Este número é então somado ao total de ataques.

A vantagem da heurística 1 em relação a heurística 2 é que ela é mais rápida, não precisa percorrer todo o estado. Além disso a heurística 1 gera menos estados na expansão do nó do que a heurística 2.

Com relação a obtenção de soluções, a heurística 2 fornece soluções mais próximas da ótima para um maior número de configurações iniciais do que a heurística 1.

Análise das propriedades do algoritmo em face do problema particular e das heurísticas

Dependendo do estado inicial e da heurística empregada o algoritmo pode encontrar uma solução ótima (8 rainhas no tabuleiro sem ataque entre elas), uma solução intermediária (8 rainhas com algumas sem ataque) ou encontrar uma solução ruim (8 rainhas atacando).

O problema do Hill-Climbing é justamente este, pode ser que ele não encontre a solução que se espera.

Uma vantagem do algoritmo é que este não consome muita memória pois não armazena todos os nós expandidos, apenas o nó que melhora o estado atual (o nó que possue melhor heurística do que a do estado atual).

Uma característica desta implementação é que é feita uma otimização em que os estados promissores que não apresentam uma heurisita que melhore a atual não chegam a entrar na lista de possiveis nós para expansão. Isto representa uma economia de memória.
 

Execução - Casos de teste
 

Execução:

As várias versões foram compiladas e executadas no modo DOS, devido as restrições de memória e tempo impostas pelo interpretador Prolog. De posse do arquivo executável basta digitar na linha de comando o nome do arquivo para executá-lo.

O programa principal foi estruturado da seguinte forma: em primeiro lugar faz alguns testes pré-definidos e em seguida permite que o usuário entre com alguns casos de teste. Para encerrar o programa basta entrar com "stop".
 

Casos de teste:

Foram feitas execuções dos mesmos casos de teste para cada versão e cada heurística.
 

Versão 1 - Heurística 1

rainhasv1h1

[(1 , 1),(4 , 2),(3 , 3),(1 , 4),(7 , 5),(3 , 6),(7 , 7),(5 , 8)] -> [(1 , 1), (6 , 2),(8 , 3),(3 , 4),(7 , 5),(4 , 6),(2 , 7),(5 , 8)]

[(1 , 1),(2 , 2),(3 , 3),(4 , 4),(5 , 5),(6 , 6),(7 , 7),(8 , 8)] -> [(1 , 1), (2 , 2),(3 , 3),(4 , 4),(5 , 5),(6 , 6),(7 , 7),(8 , 8)]

[(1 , 1),(1 , 2),(1 , 3),(1 , 4),(1 , 5),(1 , 6),(1 , 7),(1 , 8)] -> [(1 , 1), (6 , 2),(1 , 3),(1 , 4),(7 , 5),(5 , 6),(8 , 7),(2 , 8)]

[(1 , 1),(2 , 1),(3 , 1),(4 , 1),(5 , 1),(6 , 1),(7 , 1),(8 , 1)] -> [(1 , 5), (2 , 1),(3 , 6),(4 , 4),(5 , 7),(6 , 1),(7 , 8),(8 , 2)]

[(1 , 1),(2 , 2),(3 , 3),(4 , 4),(5 , 5),(6 , 6),(2 , 7),(1 , 8)] -> [(6 , 1), (2 , 2),(3 , 3),(7 , 4),(5 , 5),(4 , 6),(8 , 7),(1 , 8)]

[(5 , 1),(4 , 2),(3 , 3),(2 , 4),(6 , 4),(5 , 5),(4 , 6),(7 , 3)] -> [(5 , 1), (7 , 2),(2 , 3),(3 , 5),(6 , 4),(1 , 6),(4 , 8),(8 , 7)]

[(2 , 2),(3 , 3),(7 , 2),(6 , 3),(3 , 6),(2 , 7),(6 , 6),(7 , 7)] -> [(3 , 2), (1 , 3),(7 , 1),(8 , 5),(5 , 6),(2 , 7),(6 , 4),(4 , 8)]

[(1 , 1),(6 , 2),(8 , 3),(3 , 4),(7 , 5),(4 , 6),(2 , 7),(5 , 8)] -> [(1 , 1), (6 , 2),(8 , 3),(3 , 4),(7 , 5),(4 , 6),(2 , 7),(5 , 8)]

Estado Inicial: [(2,2), (3,3), (7,2), (6,3), (3,6), (2,7), (6,6), (7,7)].

Estado Final: [(3 , 2),(1 , 3),(7 , 1),(8 , 5),(5 , 6),(2 , 7),(6 , 4),(4 , 8)]

Estado Inicial: stop.

rainhasv1h2

[(1 , 1),(4 , 2),(3 , 3),(1 , 4),(7 , 5),(3 , 6),(7 , 7),(5 , 8)] -> [(1 , 1), (4 , 2),(6 , 3),(3 , 4),(7 , 5),(2 , 6),(8 , 7),(5 , 8)]

[(1 , 1),(2 , 2),(3 , 3),(4 , 4),(5 , 5),(6 , 6),(7 , 7),(8 , 8)] -> [(6 , 1), (3 , 2),(6 , 3),(4 , 4),(1 , 5),(8 , 6),(5 , 7),(7 , 8)]

[(1 , 1),(1 , 2),(1 , 3),(1 , 4),(1 , 5),(1 , 6),(1 , 7),(1 , 8)] -> [(8 , 1), (6 , 2),(3 , 3),(1 , 4),(7 , 5),(5 , 6),(8 , 7),(2 , 8)]

[(1 , 1),(2 , 1),(3 , 1),(4 , 1),(5 , 1),(6 , 1),(7 , 1),(8 , 1)] -> [(1 , 5), (2 , 1),(3 , 6),(4 , 4),(5 , 7),(6 , 1),(7 , 8),(8 , 2)]

[(1 , 1),(2 , 2),(3 , 3),(4 , 4),(5 , 5),(6 , 6),(2 , 7),(1 , 8)] -> [(6 , 1), (3 , 2),(1 , 3),(7 , 4),(5 , 5),(8 , 6),(2 , 7),(4 , 8)]

[(5 , 1),(4 , 2),(3 , 3),(2 , 4),(6 , 4),(5 , 5),(4 , 6),(7 , 3)] -> [(5 , 1), (7 , 2),(2 , 3),(4 , 8),(6 , 4),(3 , 5),(1 , 6),(8 , 7)]

[(2 , 2),(3 , 3),(7 , 2),(6 , 3),(3 , 6),(2 , 7),(6 , 6),(7 , 7)] -> [(5 , 1), (4 , 3),(8 , 2),(3 , 5),(1 , 4),(2 , 7),(6 , 6),(7 , 8)]

[(1 , 1),(6 , 2),(8 , 3),(3 , 4),(7 , 5),(4 , 6),(2 , 7),(5 , 8)] -> [(1 , 1), (6 , 2),(8 , 3),(3 , 4),(7 , 5),(4 , 6),(2 , 7),(5 , 8)]

Estado Inicial: [(2,2), (3,3), (7,2), (6,3), (3,6), (2,7), (6,6), (7,7)].

Estado Final: [(5 , 1),(4 , 3),(8 , 2),(3 , 5),(1 , 4),(2 , 7),(6 , 6),(7 , 8)]

Estado Inicial: stop.

rainhasv2h1

[(1 , 1),(4 , 2),(3 , 3),(1 , 4),(7 , 5),(3 , 6),(7 , 7),(5 , 8)] -> [(1 , 1), (6 , 2),(8 , 3),(3 , 4),(7 , 5),(4 , 6),(2 , 7),(5 , 8)]

[(1 , 1),(2 , 2),(3 , 3),(4 , 4),(5 , 5),(6 , 6),(7 , 7),(8 , 8)] -> [(1 , 1), (2 , 2),(3 , 3),(4 , 4),(5 , 5),(6 , 6),(7 , 7),(8 , 8)]

[(1 , 1),(1 , 2),(1 , 3),(1 , 4),(1 , 5),(1 , 6),(1 , 7),(1 , 8)] -> [(1 , 1), (6 , 2),(1 , 3),(1 , 4),(7 , 5),(5 , 6),(8 , 7),(2 , 8)]

[(1 , 1),(2 , 1),(3 , 1),(4 , 1),(5 , 1),(6 , 1),(7 , 1),(8 , 1)] -> [(1 , 1), (2 , 1),(3 , 1),(4 , 1),(5 , 1),(6 , 1),(7 , 1),(8 , 1)]

[(1 , 1),(2 , 2),(3 , 3),(4 , 4),(5 , 5),(6 , 6),(2 , 7),(1 , 8)] -> [(6 , 1), (2 , 2),(3 , 3),(7 , 4),(5 , 5),(4 , 6),(8 , 7),(1 , 8)]

[(5 , 1),(4 , 2),(3 , 3),(2 , 4),(6 , 4),(5 , 5),(4 , 6),(7 , 3)] -> [(5 , 1), (4 , 2),(3 , 3),(2 , 4),(6 , 4),(8 , 5),(1 , 6),(7 , 3)]

[(2 , 2),(3 , 3),(7 , 2),(6 , 3),(3 , 6),(2 , 7),(6 , 6),(7 , 7)] -> [(2 , 2), (3 , 3),(7 , 2),(6 , 3),(3 , 6),(2 , 7),(6 , 6),(7 , 7)]

[(1 , 1),(6 , 2),(8 , 3),(3 , 4),(7 , 5),(4 , 6),(2 , 7),(5 , 8)] -> [(1 , 1), (6 , 2),(8 , 3),(3 , 4),(7 , 5),(4 , 6),(2 , 7),(5 , 8)]

Estado Final: [(2 , 2),(3 , 3),(7 , 2),(6 , 3),(3 , 6),(2 , 7),(6 , 6),(7 , 7)]

Estado Inicial: stop.

rainhasv2h2

[(1 , 1),(4 , 2),(3 , 3),(1 , 4),(7 , 5),(3 , 6),(7 , 7),(5 , 8)] -> [(1 , 1), (4 , 2),(6 , 3),(3 , 4),(7 , 5),(2 , 6),(8 , 7),(5 , 8)]

[(1 , 1),(2 , 2),(3 , 3),(4 , 4),(5 , 5),(6 , 6),(7 , 7),(8 , 8)] -> [(6 , 1), (3 , 2),(6 , 3),(4 , 4),(1 , 5),(8 , 6),(5 , 7),(7 , 8)]

[(1 , 1),(1 , 2),(1 , 3),(1 , 4),(1 , 5),(1 , 6),(1 , 7),(1 , 8)] -> [(8 , 1), (6 , 2),(3 , 3),(1 , 4),(7 , 5),(5 , 6),(8 , 7),(2 , 8)]

[(1 , 1),(2 , 1),(3 , 1),(4 , 1),(5 , 1),(6 , 1),(7 , 1),(8 , 1)] -> [(8 , 1), (8 , 1),(8 , 1),(8 , 1),(8 , 1),(8 , 1),(8 , 1),(8 , 1)]

[(1 , 1),(2 , 2),(3 , 3),(4 , 4),(5 , 5),(6 , 6),(2 , 7),(1 , 8)] -> [(6 , 1), (3 , 2),(1 , 3),(7 , 4),(5 , 5),(8 , 6),(2 , 7),(4 , 8)]

[(5 , 1),(4 , 2),(3 , 3),(2 , 4),(6 , 4),(5 , 5),(4 , 6),(7 , 3)] -> [(5 , 1), (3 , 2),(8 , 3),(6 , 4),(6 , 4),(4 , 5),(2 , 6),(8 , 3)]

[(2 , 2),(3 , 3),(7 , 2),(6 , 3),(3 , 6),(2 , 7),(6 , 6),(7 , 7)] -> [(7 , 2), (3 , 3),(7 , 2),(3 , 3),(5 , 6),(8 , 7),(5 , 6),(8 , 7)]

[(1 , 1),(6 , 2),(8 , 3),(3 , 4),(7 , 5),(4 , 6),(2 , 7),(5 , 8)] -> [(1 , 1), (6 , 2),(8 , 3),(3 , 4),(7 , 5),(4 , 6),(2 , 7),(5 , 8)]

Estado Inicial: [(2,2), (3,3), (7,2), (6,3), (3,6), (2,7), (6,6), (7,7)].

Estado Final: [(7 , 2),(3 , 3),(7 , 2),(3 , 3),(5 , 6),(8 , 7),(5 , 6),(8 , 7)]

Estado Inicial: stop.

Versão 2 : Heurística1 e Heurística2 (roda em Amzi 4.1)