Universidade de São Paulo   Instituto de Ciências Matemáticas e de Computação   Departamento de Ciências da Computação e Estatística   Primeiro Semestre de 1999	SCE 5774 - Introdução à Inteligência Artificial  Profa.: Sandra Maria Aluísio   sandra@icmsc.sc.usp.br
	Carlos A. Estombelo Montesco  cestombe@icmsc.sc.usp.br  Pastor W. Gonzales Taco    pastor@sc.usp.br

Conclusões
Recomendações

Bibliografia

1. Introdução

Os algoritmos de busca bidirecional tem o potencial  de serem os mais eficientes quando comparados a suas contrapartes os algoritmos unidirecionais. Na verdade isto pode ser considerado quando o tamanho da árvore de busca é tomado como um indicador do custo computacional envolvido, isto é quanto maior a arvore mais nós podem ser expandidos e maior será o esforço de busca. Desde que a arvore tenha uma tendência de incremento exponencial como seus incrementos em profundidade, este será usualmente o caso no qual a soma das longitudes dos dois pequenos arvores de busca (a busca bidirecional de forward e backward) é menor que o tamanho da arvore de busca em largura da busca unidirecional. Além disso reduzindo o numero total de nós expandindose sem igual, menores árvores de procura também oferecem a vantagem de menor custo computational na escolha de menores jogos de nodos abertos. Alguns trabalhos atestam à promessa de espaços de procura menores usando algoritmos bidirecionais (Kwa, 1989). Outra motivação é a substancial redução no tempo de funcionamento pela implementação da busca bidirecional em paralelo. Porém, isto não significa que seu algoritmo unidirecional rodará mais rapidamente, isto dependerá do computacional overheads envolvido no algoritmo bidirecional.
 

2.1 O Uso da Lógica na Resolução de Problemas

Segundo Nilson (1971), frequentemente a solução de um problema qualquer requer a ajuda de uma análise lógica. Algumas vezes  as análises mostram que esses problemas são irresoluveis. Por exemplo, no caso do 15 Puzzle, é possivel provar que o estado inicial (Figura 1a) não pode produzir a configuração da meta (Figura 1b) em função da configuração do estado inicial.
 

Assim um completo tratamento de tecnicas de redução-problema, deverá incluir uma discussão de métodos mecánicos de busca de prova. Algums desses métodos usam estrategias de busca que são similares a os discutidos nas abordagens dos espaços-estados e da redução-problema.

Porém, muitos dos quebra-cabeça existentes considerados como problemas reais requerem da análise de bom senso, podendo em princípio possuir um formalismo lógico o qual permite resolve-los através de técnicas de busca de prova.
 

2. Busqueda Bidirecional

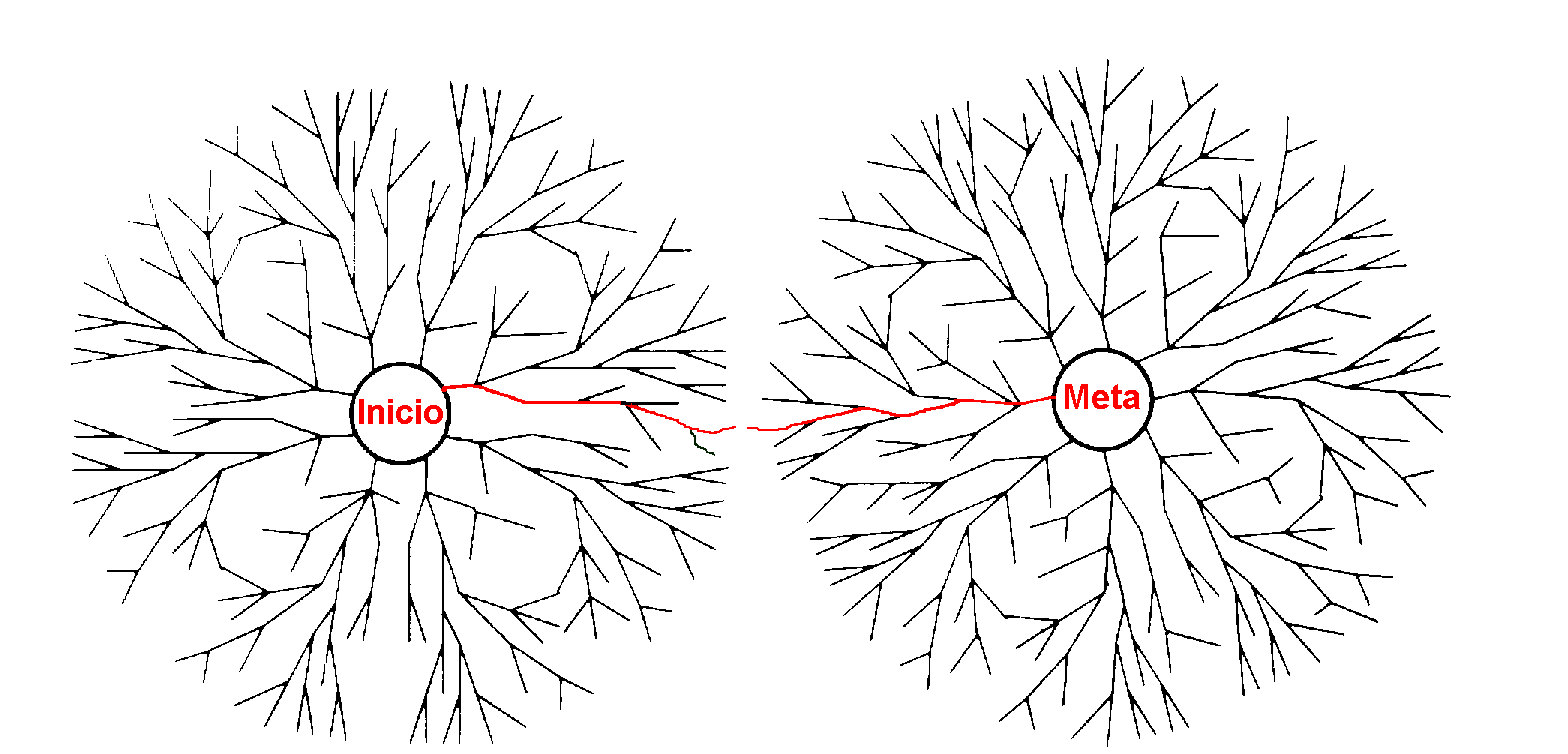
A busca bidirecional é basicamente uma busca simultânea que começa no estado inicial e que retrocede a partir da meta, finalizando quando as ambas buscas se encontram em algum ponto intermédio (Figura 2.) No caso dos problemas cujo fator de ramificação é b em ambas as direções, a busca bidirecional pode ser muito útil (Russell & Norvig, 1996). Se em forma geral assumimos a existência de uma solução geral cuja profundidade é d, então a solução estará a O(2b^(d/2)) = O(b^(d/2)) passos, dado que nas buscas para adiante (top-down) e atras (bottom-up), somente percorresse a metade do trajeto. Podemos entender melhor esta situação através de um exemplo real: se b = 10 e d = 6, uma busca preferencial por largura produzirá 1 111, 111 (um milhão cento onze mil e cento onze) nós. Entretanto, uma busca bidirecional terá êxito quando cada uma das direções de busca está a uma profundidade 3, em cujo caso gerasse 2 222 (dois mil e duzentos vente e dos) nós. Na teoria isso é fabuloso, mas antes da possivle implantação do algoritmo, é necessário resolver várias situações as quais podem serem resumidas em:

• O mais importante é: O que significa fazer a busca "buttom-up" a partir da meta?. Define-se os predecessores de um nó n como todos aqueles nós cujo sucessor é n.  A busca "bottom-up" significa a sucessiva geração de predecessores a partir do nó meta.
• Se todos os operadores são reversíveis, os conjuntos do predecessor e sucessor são idênticos. Em alguns problemas, o cálculo dos predecessores pode resultar muito difícil.
• O que fazer quando são vários os possíveis estados meta?. Em caso de contar com uma lista explícita dos estados meta, podemos aplicar uma função de predecessor a esses conjuntos de estados meta da mesma forma como é aplicada a função do sucessor em uma busca a partir do estado inicial. Se somente possuímos uma descrição do conjunto, sendo que é possível ter uma idéia dos "conjuntos de estados que poderiam gerar o conjunto meta", isto resultaria num procedimento enganoso. Assim, por exemplo, poderíamos indagar quais seriam o estados a serem considerados predecessores para obter o estado final que coincida com a configuração meta do Puzzle de 8 fichas?
• É necessário ter uma forma eficiente de verificação de cada um dos novos nós para comprovar se já estão na árvore de busca da outra metade da busca.
• Temos de definir o tipo de busca a realizar-se em cada uma das metades. Por exemplo na Figura 2, mostra-se duas buscas preferenciais por largura. Será esta a melhor opção?

3. Comparação das Diversas Estratégias de Busca

Na Tabela 1, a seguir comparam-se as seis estratégias de busca em função dos critérios de avaliação.
 

4. Resolução do Problema Bidirecional

As clausulas de Horn (um programa em PROLOG é descrito como uma série de definições lógicas, sendo que cada uma delas é uma cláusula horn)  que descrevem uma típica resolução de problemas podem ser classificadas dentro de três tipos (Kowalski, 1979):

a) Procedimentos de propósito geral (incluem asserções) com a descrição do domínio do problema;
b) Asserções de problemas específicos, os que expressam a hipótese do problema a ser resolvido, e
c) A declaração do objetivo o qual expressa esse mesmo problema.

A maioria dos procedimentos de prova de "botom-up"  não distingue entre os diferentes tipos de asserções. Como resultado estes geralmente conduzem a comportamentos de combinação explosiva, gerando asserções que seguem desde uma descrição geral do domínio do problema em adição, para asserções as quais seguem das suposições do problema particular em tratamento.

Um critério útil para combinar problemas específicos  de procura "botom-up" com procura "top-dowm" é uma variação de uma proposta de Pohl (1972)  apud. Kowalski (1979) para problemas de procura de rotas:

                  "Para todo passo escolher a direção de conclusão que dá lugar ao ultimo numero de alternativas"
Na direção "top-dowm" o numero de alternativas é  um numero pequeno de procedimentos os quais se emparelham ao sub-objetivo selecionado em um objetivo declarado. Na direção "butom-up", esto é um pequeno numero de asserções as que podem ser derivadas de uma asserção. O critério de Pohl é mostrado na Figura 3, a seguir como o problema de procura de rotas:

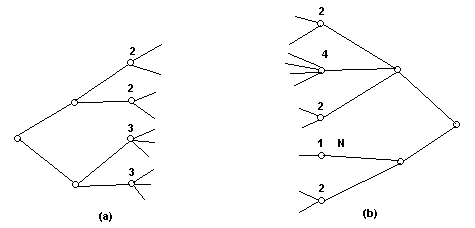
O numero seguinte de cada nó indica o numero dos nós sucessores. O critério de Pohl seleciona a direção associada com a geração do sucessor de N (Fig. 3b). Dada a previa formulação do problema de procura de rotas, a procura de rotas bidirecional é realizada pela combinação das procuras "top-dowm" e "bottom-up".
 

5. Uma Notação para Descrever a Solução doProblema Bidirecional

Para a distinção entre o "bottom-up" e "top-dowm", pode ser usado o desenho de flechas para indicar a direção da procura. Para cada par de átomos emparelhados na configuração inicial de clausulas (das quais um é a condição e o outro é a conclusão) uma flecha é dirigida de um átomo ao outro.
Para a inferência top-dowm as flechas são dirigidas das condições às conclusões. Para o problema dos Grandparent, obtemos a seguinte representação:

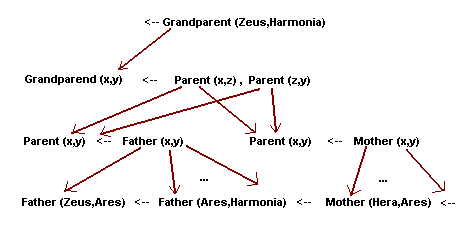
Para a inferência botom-up, as flechas são dirigidas das conclusões às condições, como mostrado a seguir:
 

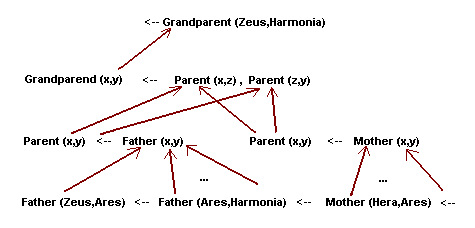
A definição dos Grandparent pode também ser usada em uma combinação top-down, bottom-up, sendo que as diferentes combinações podem ser representadas usando números que indiquem a seqüência. Para simplificar mostraremos somente a notação associada com a definição dos Grandparent, onde a combinação de direções será:

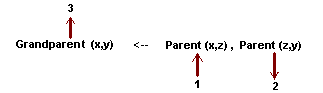
 a qual representa o algoritmo seguinte:
 
           1) esperar até x seja confirmado como parente de z, então
           2) encontrar um filho y de z, e finalmente
           3) confirmar que x é Grandparent de y.

A combinação indicada por:

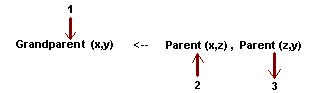
representará o algoritmo seguinte:

           1) responder ao problema mostrando que x é o Grandparent de y,
           2) esperando até x ser confirmado como padre de z, e então
           3) tente mostrar que z é padre de y.
 

6. Problema do Jogo das Oito Fichas (8 Puzzle)

O jogo das oito fichas pertence à família dos blocos deslizáveis (Puzzles). Está classe geral é do tipo NP completa, sendo possível achar métodos de solução como os dos algoritmos de busca em profundidade, busca em largura, uma combinação de ambos, ou técnicas de busca como a busca bidirecional. Sendo que este tipo de jogos permite o teste de novos algoritmos em Inteligência Artificial.

O quebra-cabeça de 8 ou jogo das oito fichas, cujo exemplo mostra-se na Figura 4a, consiste em um tabuleiro quadrado com nove divisões, onde são colocadas oito fichas quadradas, numeradas de 1 a 8, e um espaço em vazio. A ficha adjacente ao espaço em vazio pode ser deslocada para aquele espaço. O objetivo é obter, a partir de uma posição inicial (configuração mostrada na Figura 4a), uma posição meta (configuração mostrada na Figura 4b), deslocando as peças até que elas atinjam o local desejado. Um estrategia importante é obtida ao descobrir que em lugar de usar operadores como "desliza a ficha 3 ao espaço vazio", é melhor utilizar operadores como "o espaço vazio pode trocar seu lugar com a ficha que está à esquerda", dado que existe menos operadores como o anterior. Isto nos permite chegar a seguinte formulação de condições básicas para resolução do problema:

• Estados: A descrição de um estado especifica a localização de cada uma das oito fichas em um dos nove lugares disponíveis. Por motivos de eficiência conbem incluir a localização do espaço vazio
• Operadores: O espaço vazio pode moverse à esquerda, à direita, acima ou abaixo.
• Prova da meta: O estado deve coincidir com a configuração da meta mostrada na Figura 4b.
• Custo da Rota: Cada passo custa 1 (um), porem o custo da rota corresponde ao comprimento da rota.

A recuperabilidade de um problema tem papel importante na determinação da complexidade da estrutura de controle necessária para a solução do problema. Os problemas recuperáveis podem ser solucionados através de uma estrutura de controle ligeiramente mais complicada, que às vezes comete erros. O retrocesso será necessário para recuperar estes erros, logo a estrutura de controle precisa ser implementada usando-se uma pilha de cima para baixo, na qual as decisões são gravadas caso precisem ser desfeitas mais tarde.
 

6.1 Raciocínio para Frente Versus Raciocínio para Trás

O objetivo de um procedimento de busca é descobrir um caminho através de um espaço de problema, a partir de uma configuração inicial até um estado-meta. Embora o PROLOG só busque a partir de um estado-meta, uma busca na verdade pode prosseguir em duas direções:

• Para frente, a partir dos estados iniciais;
• Para trás, a partir dos estados-meta.

Considere o problema de resolver uma determinada instância do quebra-cabeça de 8. As regras a serem usadas para solucionar o quebra-cabeça podem ser escritas como mostra a Figura 4 Usando essas regras, podemos tentar solucionar o quebra-cabeça mostrado na Figura4. de uma destas duas maneiras:
 

• Raciocinar para frente a partir dos estados inicias. Comece criando uma árvore de sequencias de movimentos, que podem ser soluções, começando com a configuração inicial na raiz da árvore. Gere o próximo nível da árvore encontrando todas as regras cujos lados esquerdos casem como o nó-raiz e usando os lados direitos para criar as novas configurações. Gere o próximo nível pegando cada nó gerado no nível anterior e aplicando a ele todas as regras cujos lados esquerdos casem. Continue até gerar uma configuração que case com o estado-meta.

• Raciocinar para trás a partir dos estados-meta. Comece criando uma árvore de sequencias de movimentos que possam ser soluções começando com a(s) configuração(ões)-meta na raiz da árvore. Gere o próximo nível da árvore encontrando todas as regras cujos lados direitos casem com o nó-raiz. São essas as regras que, se pudésemos aplicá-las, gerariam o estado que desejamos. Use os lados esquerdos das regras par gerar os nós neste segundo nível da árvore. Gere o próximo nível da árvore pegando cada nó do nível anterior e encontrando todas as regras cujos lados direitos casem com cada um deles. Depois use os lados esquerdos correspondientes para gerar os novos nós. Continue até gerar um nó que case com o estado inicial. Este método de raciocínio para trás a partir do estado final desejado é  normalmente chamado de raciocínio  dirigido pelos objetivos.

Podemos também buscar tanto simultaneamente para frente a partir do estado inicial quanto para trás a partir do objetivo até que dois percursos se encomtrem em algum lugar no meio do caminho. Esta estratégia é chamada de busca bidirecional. Ela parece interessante se o número de nós em cada passo cresce exponencialmente em relação ao número de passos que já foram dados. Resultados empíricos (Pohl, 1971) sugerem que no caso de buscas cegas, esta estratégia de dividir-e-conquistar é realmente eficaz. A Figura 5, mostra porque a busca bidirecional pode ser ineficaz. As duas buscas podem passar uma pela outra, resultando em mais um trabalho do que teria sido necessário para uma delas, por si só, terminar. Entretanto, se etapas isoladas para frente e para trás forem cumpridas conforme especificado por um programa cuidadosamente construído para explorar cada uma dessas situações exatamente nas situações em que elas são mais lucrativas, os resultados poderão ser mais encorajadores. Na verdade, muitas aplicações de sucesso em IA foram elaborados usando-se uma combinação do raciocínio para frente e para trás, e a maioria dos ambientes de programação em IA fornece suporte explícito para esse raciocínio híbrido.
 

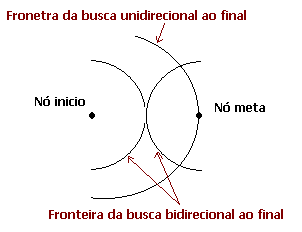
Embora em princípio, o mesmo conjunto de regras possa ser usado tanto para o raciocínio para frente quanto para o raciocínio para trás, na prática ficou provado que é útil definir duas classes de regras, cada uma delas codificando um determinado tipo de conhecimento:

• Regras para frente, que codificam conhecimentos sobre como responder a certas configurações de entrada.
• Regras para trás, que codifican conhecimentos sobre como atingir determinados objetivos.

6.2 Combinar o Raciocínio para Frente e Para Trás

Ás vezes, certos aspectos de um problema são mais bem abordados via encadeamento para frente, e outros aspectos pelo encadeamento para trás. Consideresse um programa de diagnóstico médico com encadeamento para frente. Ele pode aceitar vinte e tantos fatos sobre a condição de um paciente, e depois encadear para frente, com base nesses fatos, para tentar deduzir a natureza e/ou a causa da doença. Agora suponha que, em um determinado ponto, o lado esquerdo de uma regra esteja quase satisfeito - digamos, nove entre dez de suas precondições foram satisfeitas. Pode valer a pena aplicar o raciocínio para trás de maneira direcionada para satisfacer a décima precondição em vez de esperar que o encadeamento para frente forneça o fato por acidente. Ou talvez a décima condição exija mais testes médicos. Nesse caso , o encadeamento para trás pode ser usado para consultar o usuário.

Saber se é possível ou não usar as mesmas regras para o raciocínio para frente e para trás também depende da forma das regras em si. Se tanto os lados esquerdos quanto os lados direitos contêm apenas declarações, então o encadeamento para frente pode casar as declarações no lado esquerdo de uma regra e acrescentar à descrição do estado a declaração do lado direito. Mas, se procedimentos arbitrários forem permitidos nos lados direitos das regras, então elas não serào reversíveis. algumas linguagens de regras de produção permiten apenas regras reversíveis; outras não. Quando regras irreversíveis são usadas, então é preciso que haja um acordo sobre a direção da busca no momento em que as regras forem escritas. Mas, conforme sugerimos, isto e com frequencia um recurso útil, porque permite que o criador da regra acrescente conhecimentos de controle às própias regras.
 

6.3 Casamento

Até aqui, descrevemos o proceso de uso de busca para solucionar problemas como sendo a aplicação de regras apropiadas a estados isolados de problemas, para gerar novos estados aos quais as regras podem então ser aplicadas, e assim por diante, até ser encontradas uma solução. Sugerimos que a busca inteligente deve envolver a escolha de regras que possam ser aplicadas em um determinado ponto, e que têm grande chance de levar  a uma solução. Mas foi dito pouco sobre como extrair de un conjunto inteiro de regras aquelas que podem ser aplicadas em um determinado ponto. Esta operação requer algum tipo de casamento entre o estado atual e a precondição das regras. Como isto deve ser feito? A resposta a esta pergunta pode ser crucial para o sucesso de um sistema baseado em regras. Temos algumas propostar a seguir :

• Indexação
• Casamento com Varíaveis
• Casamento complexo e aproximado

O resultado do processo de casamento é uma lista de regras cujos antecedentes casaram com a descrição do estado atual, juntamente com quaisquer ligações da variáveis geradas pelo mesmo processo. É responsabilidade do método de busca decidir sobre a ordem em que as regras serão aplicadas. Mas, ás vezes, é útil incorporar parte da tomada de decisão ao processo de casamento. Esta fase é então chamada de resolução de conflitos. Neste caso do quebra-cabeça de 8 a abordagen usado  para o problema da resolução de conflitos em um sistema de produção e Preferência Baseadas em Estados, quer dizer os estados são comparados em cada nivel de exploração.
 

7. Algoritmo de Busca Bidirecional

Para execusão do programa da busca bidirecional recomenda-se aumentar a capacidade de memória ao trabalhar com LPA-PROLOG, digitando no ambiente DOS:

    C:\...\pro386w /h16000
 

/* Busca em Profundidade x Largura  */
/* Definição de Operadores Utilizados no Algoritmo, e Bases de Dados Dinâmicas para a Contagem de Nós Expandidos eTempo de Execusão*/

:- op(35, xf,  e_a_meta     ).
:- op(35, xfx, atinge_a_meta).
:- op(35, xfx, transforma   ).
:- op(30, xfx, em           ).
:- op(35, xfx, nao_produz_circulos_em).
:- dynamic(countinicio/1).
:- dynamic(countmeta/1).
:- dynamic(tempo/1).

/********************************************************************/
/********************* Predicado Principais *************************/

/*Resolva o Predicado Principal para Iniciar a Busca Bidirecional, Onde inicia as Bases de Dados Dinâmicas em Zero*/

resolva :- init_dynamic,
 estado_inicial( Inicio ),  Meta e_a_meta,  /*Carrega o estado inicial e o estado meta nas respectivas variaveis*/
 busca_bidirectional( [[ r(raiz, Inicio) ]], [[r(meta, Meta)]], SolucaoDeInicio, SolucaoDeMeta ), /*Inicia a Busca Bidirecional, interccalando os casamentos de busca*/
 imprimatempo,
 imprima( SolucaoDeInicio ), nl, nl,
 imprima( SolucaoDeMeta ), nl.

/*Pergunta se tem a rota de solução para cada iteração*/
busca_bidirectional( LLSolDeInicio, LLSolDeMeta, SolucaoDeInicio, SolucaoDeMeta ) :-
 procura( LLSolDeInicio, LLSolDeMeta, SolucaoDeInicio, SolucaoDeMeta ).

/*Passa ao nível seguinte gerando os filhos do nível pai, tanto para a busca da árvore de inicio como da busca da árvore de meta*/
busca_bidirectional( [HeadIni|TailIni], [HeadMeta|TailMeta], SolucaoDeInicio, SolucaoDeMeta) :-
 ache_todos( ExtensaoAteUmFilhoIni, estende_ate_filho( HeadIni, ExtensaoAteUmFilhoIni ), ExtensoesIni ),
 soma_ini(ExtensoesIni), /*Conteo dos nós expandidos desde o nó de inicio*/
 ap( ExtensoesIni, TailIni, ListaEstendidaIni ), /*Adiciona todos os nós filhos à listapara a busca em profundidade*/
 ache_todos( ExtensaoAteUmFilhoMeta, estende_ate_filho( HeadMeta, ExtensaoAteUmFilhoMeta ), ExtensoesMeta ),
 soma_meta(ExtensoesMeta), /*Conteo dos nós expandidos desde o nó meta*/
 ap( TailMeta, ExtensoesMeta, ListaEstendidaMeta ), /*Adiciona todos os nós filhos para a busca em largura*/
 busca_bidirectional( ListaEstendidaIni, ListaEstendidaMeta, SolucaoDeInicio, SolucaoDeMeta ).

/*Extende tudos os nós filhos de um nó determinado*/
estende_ate_filho( [r(Ramo,N)|Trajetoria], [r(Op,Filho), r(Ramo,N)|Trajetoria] ) :-
 operacao( Op ) transforma N em Filho,
 not Filho nao_produz_circulos_em Trajetoria.

/*Verifica que não existam ciclos na rota*/
Estado nao_produz_circulos_em Trajetoria :-
 membro( r( Operacao, Estado ), Trajetoria ).

/* Nesta Linha debe-se fazer a comparação Bidirecional */
r( RamoIni, ML ) atinge_a_meta r( RamoMeta, MP ):-
 ML = MP.
 
/* nova comparação */
procura( LLSolDeInicio, LLSolDeMeta, SolucaoDeInicio, SolucaoDeMeta ) :-
 procura2( LLSolDeInicio, LLSolDeMeta, SolucaoDeInicio, SolucaoDeMeta ).

procura( [_|LTailSolIni] , LLSolDeMeta, SolucaoDeInicio, SolucaoDeMeta ) :-
 procura( LTailSolIni, LLSolDeMeta, SolucaoDeInicio, SolucaoDeMeta ).

/*Comparação dos nós de inicio com os nós meta, em função do tipo de busca bidirecional*/
procura2( [[ HeadIni|TailIni ] | _], [[ HeadMeta|TailMeta ] | _], SolucaoDeInicio, SolucaoDeMeta ) :-
 HeadIni atinge_a_meta HeadMeta,
 SolucaoDeInicio = [ HeadIni  | TailIni  ],
 SolucaoDeMeta   = [ HeadMeta | TailMeta ], !.

procura2( LLSolDeInicio, [_|LTailMeta], SolucaoDeInicio, SolucaoDeMeta ) :-
 procura2( LLSolDeInicio , LTailMeta, SolucaoDeInicio, SolucaoDeMeta ).

/*********************************************************************/
/*********************** Base de Conhecimentos ***********************/

operacao(esq)  transforma [A,*,C,D,E,F,H,I,J] em [*,A,C,D,E,F,H,I,J].
operacao(esq)  transforma [A,B,C,D,*,F,H,I,J] em [A,B,C,*,D,F,H,I,J].
operacao(esq)  transforma [A,B,C,D,E,F,H,*,J] em [A,B,C,D,E,F,*,H,J].
operacao(esq)  transforma [A,B,*,D,E,F,H,I,J] em [A,*,B,D,E,F,H,I,J].
operacao(esq)  transforma [A,B,C,D,E,*,H,I,J] em [A,B,C,D,*,E,H,I,J].
operacao(esq)  transforma [A,B,C,D,E,F,H,I,*] em [A,B,C,D,E,F,H,*,I].

operacao(cima)  transforma [A,B,C,*,E,F,H,I,J] em [*,B,C,A,E,F,H,I,J].
operacao(cima)  transforma [A,B,C,D,*,F,H,I,J] em [A,*,C,D,B,F,H,I,J].
operacao(cima)  transforma [A,B,C,D,E,*,H,I,J] em [A,B,*,D,E,C,H,I,J].
operacao(cima)  transforma [A,B,C,D,E,F,*,I,J] em [A,B,C,*,E,F,D,I,J].
operacao(cima)  transforma [A,B,C,D,E,F,H,*,J] em [A,B,C,D,*,F,H,E,J].
operacao(cima)  transforma [A,B,C,D,E,F,H,I,*] em [A,B,C,D,E,*,H,I,F].

operacao(dir)  transforma [A,*,C,D,E,F,H,I,J] em [A,C,*,D,E,F,H,I,J].
operacao(dir)  transforma [A,B,C,D,*,F,H,I,J] em [A,B,C,D,F,*,H,I,J].
operacao(dir)  transforma [A,B,C,D,E,F,H,*,J] em [A,B,C,D,E,F,H,J,*].
operacao(dir)  transforma [*,B,C,D,E,F,H,I,J] em [B,*,C,D,E,F,H,I,J].
operacao(dir)  transforma [A,B,C,*,E,F,H,I,J] em [A,B,C,E,*,F,H,I,J].
operacao(dir)  transforma [A,B,C,D,E,F,*,I,J] em [A,B,C,D,E,F,I,*,J].

operacao(baixo) transforma [A,B,C,*,E,F,H,I,J] em [A,B,C,H,E,F,*,I,J].
operacao(baixo) transforma [A,B,C,D,*,F,H,I,J] em [A,B,C,D,I,F,H,*,J].
operacao(baixo) transforma [A,B,C,D,E,*,H,I,J] em [A,B,C,D,E,J,H,I,*].
operacao(baixo) transforma [*,B,C,D,E,F,H,I,J] em [D,B,C,*,E,F,H,I,J].
operacao(baixo) transforma [A,*,C,D,E,F,H,I,J] em [A,E,C,D,*,F,H,I,J].
operacao(baixo) transforma [A,B,*,D,E,F,H,I,J] em [A,B,F,D,E,*,H,I,J].

/********************************************************************/
/************************ Testes  ***********************/

/*Test A*/

estado_inicial([1,2,3,4,5,6,7,8,*]).

[3,*,1,2,5,6,4,7,8] e_a_meta.
 

/*Test B*/
/*
estado_inicial([1,2,3,4,5,6,7,8,*]).

[*,3,1,2,5,6,4,7,8] e_a_meta.
*/

/*Test C*/
/*
estado_inicial([1,2,3,4,5,6,7,8,*]).

[2,3,1,*,5,6,4,7,8] e_a_meta.
*/

/*Test D*/
/*
estado_inicial([1,2,3,4,5,6,7,8,*]).

[2,3,*,1,5,6,4,7,8] e_a_meta.
*/

/* Test E */
/*
estado_inicial([1,2,3,4,5,6,7,8,*]).

[1,2,3,5,*,6,4,7,8] e_a_meta.
*/
 
 

/********************************************************************/
/************************ Predicados de Ajuda ***********************/

init_dynamic :-
 asserta(countinicio(0)), asserta(countmeta(0)),
 ticks(Tempo), asserta(tempo(Tempo)).

imprimatempo :- ticks(Tempo2), retract(tempo(Tempo)),
 write('*********** Resultados **********'),nl,nl,
 write('O Tempo Rodado em ticks :'),
 Ticks is Tempo2 - Tempo,
 write(Ticks),nl,nl.

/*Contadores da expansão dos nós de inicio e de meta*/
soma_ini([]):-!.
soma_ini([Head|Tail])  :- retract(countinicio(N)),
 Tot is N + 1, asserta(countinicio(Tot)),
 soma_ini(Tail),!.
soma_meta([]):-!.
soma_meta([Head|Tail]) :- retract(countmeta(N)),
 Tot is N + 1, asserta(countmeta(Tot)),
 soma_meta(Tail),!.
 

/*Adiciona uma lista para outra lista*/
ap([],X,X) :- !.
ap([X|Y],Z,[X|W]) :- ap(Y, Z, W).

/*Verifica se um elemento encontra-se dentro de uma lista*/
membro(X,[X|_]) :- !.
membro(X,[_|Y]) :- membro(X,Y).

ache_todos(X, Y, Z) :- findall(X, Y, Z), !.
ache_todos(_, _, []).

imprima([r(raiz,Raiz)]) :- !,
 write('Estado Inicial( Busca De Inicio - Profundidade)  : '),
 write(Raiz), write('.'),nl,
 retract(countinicio(Nos)), write('Nos Expandidos:'), write(Nos),nl.

imprima([r(meta,Meta)]) :- !,
 write('Estado Final  ( Busca De Meta   - Largura     )  : '),
 write(Meta), write('.'),nl,
 retract(countmeta(Nos)), write('Nos Expandidos:'), write(Nos),nl.

imprima([r(Ramo,Nodo)|R]) :- imprima(R), nl,
 write(Ramo), write(' e ,portanto, temos: '), nl,
 tab(4),write(Nodo), write('.').
 

8. Tipos de Busca Bidirecional Usando Largura e Profundidade

Foram definidas as seguintes combinações de busca, testadas para cada um dos tipos de 8-puzzle:

• Largura x Largura;
• Largura x Profundidade;
• Profundidade x Largura, e
• Profundidade x Profundidade.

8.1  Puzzle A:
 

 8.2  Puzzle B:
 

 8.3  Puzzle C:

 8.4  Puzzle D:
 

 8.5  Puzzle E:
 

 8.6  Análise dos Resultados Experimentais

Os esperimentos foram conduzidos por comparação pelos resultados obtidos em função dos nós expandidos em cada tipo de busqueda bidirecional, e os nós de rota de casamento. Em ambos os casos tomou-se em consideração o estado de busqueda para frente desde o inicio, e os estado de busca para trás desde a meta. Assim é possivel fazer uma comparação do tipo de busca bidirecional nos diferentes tipos de puzzle, tratando-se de determinar a variavilidade dos resultados.
 

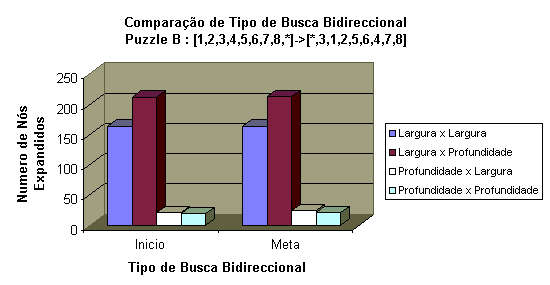
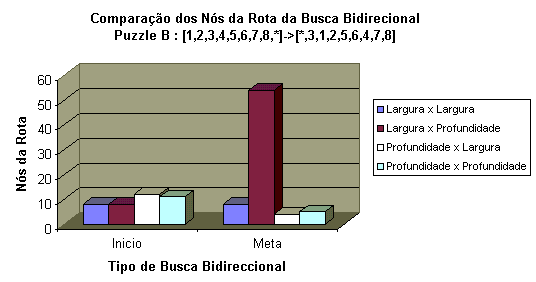
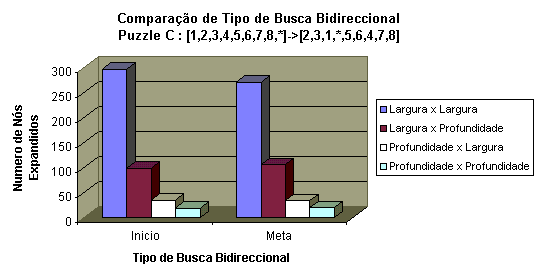
Para o Tipode Puzzle C, como observado na Figura 8, podemos afirmar que em função do numero de nós expandidos,  a combinação largura x largura gerou a maior quantidade de nós, a respeito das outras combinações, sendo esta combinação dependente da memória do computador. O caso oposto a isso é observado na combinação profundidade x profundidade, onde gerou-se o menor  numero de nós expandidos. Isso não significa que esta ultima seja uma combinação ideal, pois pode acontecer que os espaços de busca sejam distantes um do outro, impossibilitando encontrar-se, gerando assim o pior caso de busca unidirecional em ambos os sentidos de busca.

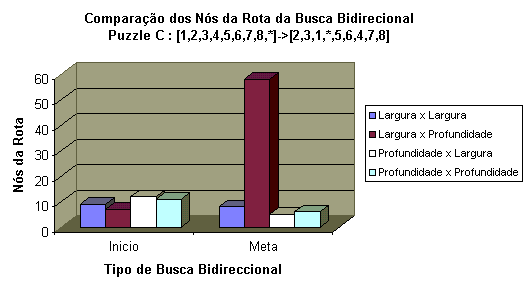
Para o caso dos número de nós da rota, no Tipode Puzzle C, podemos observar na seguinte Figura 9, este segue um comportamento muito similar ao produzido no Tipo de Puzzle B .
 

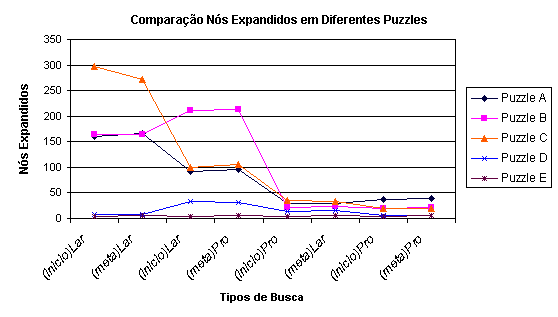
8.7 Comparação Final dos Testes para os Diferentes Tipos de Puzzle

Para efeitos de um melhor entendimento foi gerada a seguinte Figura 10, onde são comparados os numeros de Nós expandidos para cada Tipo de Puzzle, observamos que estes valores são maiores no caso da combinação largura x largura ((inicio)Lar --(meta)Lar). Além disso estes valores nos mostram a maior dificuldade do Puzzle C, a respeito do Puzzle D. Para todas os Puzzles na combinação profundidade x profundicade ((inicio)Pro--(meta)Pro) o número de nós expandidos foram poucos, sendo que isto não necesariamente seja a melhor combinação, como explicado anteriormente
.

Conclusões:
 

• Algoritmos de busca bidirecional são de especial interes porque têm o potencial para procurar pequenos espaços e reduzem significativamente o tempo de funcionamento por implementação paralela. Enquanto o último é geralmente verdade, o primeiro pode ser enganoso quando existem múltiplos caminhos de solução comparáveis.
• Aplicado de forma incorreta o método de busca bidirecional, pode originar os piores casos de busca, transformando-se em casos de busca unidirecionais onde os espaços de busca são distantes entre se.
• Com os teste aplicados, e as respectivas análises,  logrou-se diferenciar a dificuldade na solução dos diferentes tipos de Puzzle, em função do número de nós expandidos para cada caso.

• Propõe-se aprofundar na pesquisa da busca bidirecional fazendo uso de algoritmos heuristicos, como os desenvolvidos por Champeaux & Sint (1977), Kwa (1989), Manzini (1995).
• Testas outras combinações de Puzzles para acrescentar mais informações, a respeito dos resultados obtidos.

• Nilson, J. N. (1971) Problem-Solving Methods in Artificial Intelligence. McGraw-Hill, Unites Stated of America.
• Russell, S. & Norvig, P. (1996) Inteligencia Artificial: Un Enfoque Moderno. Prentice Hall, México.
• Kowalski, R. (1979) Logic for Problem Solving. Elsevier Science Publishing Co., Inc.
• Rich, E. & Knight, K. (1993) Inteligência Artificial. Makron Boks, São Paulo.

Bibliografia Referêncial:
 

• Champeaux, D & Sint, L. (1977) An Improved Bidirectional Heuristic Search ALgorithm. Journal of the Association for    Computing Machinery, vol. 24, Nº 2, pp. 177-191.
• _____________________(1977) An Optimality Theorem for a Bi-directional Heuristic Search Algorithm. The Computer Journal, vol. 20, Nº 2, pp. 148-150.
• Manzini, G. (1995) BIDA*: An Improved Perimeter Search Algorithm. Artificial Intelligence 75, pp. 347-360.
• Kwa, J. B. H. (1989) BS*: An Admissible Bidirectional Staged Heuristic Search Algorithm. Artificial Intelligence 38, pp. 95-109.
• Monard, M. C. & Nicoletti, M. C. (1993) Programa Prolog para Processamento de Listas e Aplicações. Notas Didáticas de do ICMSC, São Carlos-SP.