Projeto Mapa de quatro cores em PROLOG

O Projeto

Atribuir a cada país em um dado mapa planar uma de 4 cores de tal forma que nenhum dos vizinhos sejam pintados com a mesma cor. O teorema das 4 cores foi provado em 1976 por Appel e Haken e garante que é possível solucionar este problema usando somente 4 cores.

Por exemplo:

A Resolução

INTRODUÇÃO

O problema da coloração de mapas planares por apenas 4 cores é explicado da seguinte forma:

Em primeiro lugar deve-se transformar o mapa em um grafo planar. Deve-se atribuir vértices aos países do mapa em questão fazendo assim com que estes possam ser interpretados como pontos adjacentes e de mesma forma com seus "vizinhos".

Após efetuar a ligação entre todos os vértices, pode-se verificar quem é vizinho de quem no mapa, e é através desta lista de adjacências que é possível atribuir cores distintas para cada país vizinho.

DESENVOLVIMENTO

O mapa a seguir será tomado como base no projeto da "coloração de mapas" que será apresentado neste trabalho escrito em Delphi e em Prolog.

Mapa Exemplificado

De acordo com o mapa acima é possível se chegar a uma grafo desenhado a seguir e a partir deste ser criada uma especificada lista de adjacência , fundamental para a coloração dos "países" que são caracterizados por arestas compostas por vértices.

Grafo Países

É possível notar que nenhuma "linha de ligação" entre os vértices passa por cima de outra fato este que caracteriza o grafo planar e faz com que seja possível a utilização de apenas quatro cores para preenche-lo sem que seus adjacentes obtenham a mesma cor.

Lista de Adjacência

Vértice	Vértices Adjacentes
A	B	C	D
B	A	C	D
C	A	B	D
D	A	B	C	E
E	D

Após analisar a lista de adjacência acima pode-se criar uma tabela de cores a serem utilizadas e consequencemente cores que os adjacentes não podem utilizar.

Nesta tabela, as cores são atribuídas de acordo com o número de adjacentes que cada vértice possui. Todos os vértices são colocados em ordem de acordo com a quantidade de adjacêntes que possui, do maior para o menor e assim são atribuídas cores aos vértices. Vale ressaltar que a análise é feita através do vértice e não da cor propriamente dita. A primeira cor vai para aquele vértice que contem maior número de adjacentes. Na atribuição da segunda cor, é verificado se o segundo vértice em número de adjacentes pode possuir a mesma cor que o primeiro vértice sendo observado se este vértice é ou não adjacente so primeiro. Se for, este passa a Ter uma segunda cor. Caso contrário ele recebe a mesma cor que o primeiro vértice.

Este procedimeto é repetido até o último vértice do grafo. Vale lembrar que neste caso estamos trabalhando com um grafo de cinco vértices.

Na tabela abaixo temos uma lista de cores atribuídas de acordo com a não coinscidência de vértices. Note que preliminarmente os vértices são colocados de maneira ordenada e só depois são atribuídas cores a eles. Vejamos a seguinte tabela em etapas:

Lista de Cores possíveis à 1 de 6

Vértice	Vértices Adjacentes				Cores
D	A	B	C	E
A	B	C	D
B	A	C	D
C	A	B	D
E	D

Lista de Cores possíveis à 2 de 6

Vértice	Vértices Adjacentes					Cores
D	A	B	C	E	Verde
A	B	C	D
B	A	C	D
C	A	B	D
E	D

Lista de Cores possíveis à 3 de 6

Vértice	Vértices Adjacentes					Cores
D	A	B	C	E	Verde
A	B	C	D		Amarelo
B	A	C	D
C	A	B	D
E	D

Lista de Cores possíveis à 4 de 6

Vértice	Vértices Adjacentes					Cores
D	A	B	C	E	Verde
A	B	C	D		Amarelo
B	A	C	D		Azul
C	A	B	D
E	D

Note que sempre que existe coinscidência entre o vértice principal e um de seus adjacentes, é atribuída uma nova cor.

Lista de Cores possíveis à 5 de 6

Vértice	Vértices Adjacentes					Cores
D	A	B	C	E	Verde
A	B	C	D		Amarelo
B	A	C	D		Azul
C	A	B	D		Vermelho
E	D

Lista de Cores possíveis à 6 de 6

Vértice	Vértices Adjacentes					Cores
D	A	B	C	E	Verde
A	B	C	D		Amarelo
B	A	C	D		Azul
C	A	B	D		Vermelho
E	D				Amarelo

Após a criação da tabela final (6), podemos verificar a tabela de cores resultante, já com as qutreo cores distribuídas de maneira correta aos vértices especificados.

A seguir, a tabela final de cores:

Vértice		Cores
D	Verde
A	Amarelo
B	Azul
C	Vermelho
E	Amarelo

Com esta tabela é possível fazer com que cada "país" do mapa, formado por um conjunto de vértices interligados, possa Ter uma cor diferenrte, conforme apresentado na figura a seguir:

CONCLUSÃO

Todo e qualquer grafo planar pode ser interpretado e preenchido usando apenas quatro cores sem que as áreas vizinhas possuam coincidência de cor.

Em Delphi

Em Prolog:

Arquivo PL

podeservizinho(azul,amarelo).
podeservizinho(azul,verde).
podeservizinho(azul,vermelho).

podeservizinho(amarelo,azul).
podeservizinho(amarelo,verde).
podeservizinho(amarelo,vermelho).

podeservizinho(vermelho,amarelo).
podeservizinho(vermelho,azul).
podeservizinho(vermelho,verde).

podeservizinho(verde,amarelo).
podeservizinho(verde,azul).
podeservizinho(verde,vermelho).

colorir(Pais1,Pais2,Pais3,Pais4,Pais5) :-
                                                            podeservizinho(Pais1,Pais2),
                                                            podeservizinho(Pais1,Pais3),
                                                            podeservizinho(Pais1,Pais4),
                                                            podeservizinho(Pais1,Pais5),
                                                            podeservizinho(Pais2,Pais3),
                                                            podeservizinho(Pais2,Pais4),
                                                            podeservizinho(Pais3,Pais4),
                                                            podeservizinho(Pais4,Pais5).

Comentários

Este programa foi feito para solucionar problemas com grafos Planares ou não planares.

Este mesmo problema pode ser aplicado para qualquer número de vértices. No mapa abaixo (EUA) podemos verificar a sua coloração conforme o problema das quatro cores e este possuindo bem mais do que cinco vértices.

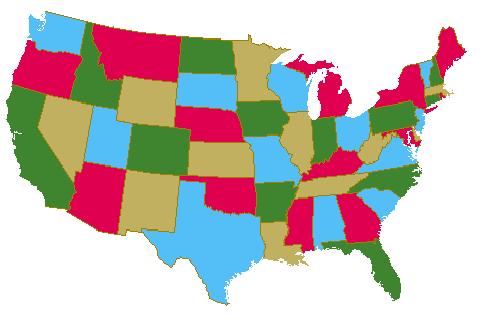
MapaEUA.jpg (20074 bytes)

Mais detalhes sobre este projeto podem ser encontrados no seguinte endereço:
http://www.math.gatech.edu/~thomas/FC/fourcolor.html

Os Testes

___________________________________________________
LPA WIN-PROLOG 3.300 - S/N 0008802080 - 04 Jun 1996
Copyright (c) 1996 Logic Programming Associates Ltd
Licensed To: USP-ICMSC-LABIC
B=64 L=64 R=64 H=255 T=421 P=1469 S=63 I=64 O=64 Kb
___________________________________________________
| ?-
# 0.00 seconds to consult cor.pl [c:\soft2\lpa\pro386w\]
| ?- colorir(Pais1,Pais2,Pais3,Pais4,Pais5).

Pais1 = azul ,
Pais2 = Pais5 = amarelo ,
Pais3 = verde ,
Pais4 = vermelho ;

Pais1 = azul ,
Pais2 = amarelo ,
Pais3 = Pais5 = verde ,
Pais4 = vermelho ;

Pais1 = azul ,
Pais2 = Pais5 = amarelo ,
Pais3 = vermelho ,
Pais4 = verde ;

Pais1 = azul ,
Pais2 = amarelo ,
Pais3 = Pais5 = vermelho ,
Pais4 = verde ;

Pais1 = azul ,
Pais2 = verde ,
Pais3 = Pais5 = amarelo ,
Pais4 = vermelho ;

Pais1 = azul ,
Pais2 = Pais5 = verde ,
Pais3 = amarelo ,
Pais4 = vermelho ;

Pais1 = azul ,
Pais2 = Pais5 = verde ,
Pais3 = vermelho ,
Pais4 = amarelo ;

Pais1 = azul ,
Pais2 = verde ,
Pais3 = Pais5 = vermelho ,
Pais4 = amarelo ;

Pais1 = azul ,
Pais2 = vermelho ,
Pais3 = Pais5 = amarelo ,
Pais4 = verde ;

Pais1 = azul ,
Pais2 = Pais5 = vermelho ,
Pais3 = amarelo ,
Pais4 = verde ;

Pais1 = azul ,
Pais2 = vermelho ,
Pais3 = Pais5 = verde ,
Pais4 = amarelo ;

Pais1 = azul ,
Pais2 = Pais5 = vermelho ,
Pais3 = verde ,
Pais4 = amarelo ;

Pais1 = amarelo ,
Pais2 = Pais5 = azul ,
Pais3 = verde ,
Pais4 = vermelho ;

Pais1 = amarelo ,
Pais2 = azul ,
Pais3 = Pais5 = verde ,
Pais4 = vermelho ;

Pais1 = amarelo ,
Pais2 = Pais5 = azul ,
Pais3 = vermelho ,
Pais4 = verde ;

Pais1 = amarelo ,
Pais2 = azul ,
Pais3 = Pais5 = vermelho ,
Pais4 = verde ;

Pais1 = amarelo ,
Pais2 = verde ,
Pais3 = Pais5 = azul ,
Pais4 = vermelho ;

Pais1 = amarelo ,
Pais2 = Pais5 = verde ,
Pais3 = azul ,
Pais4 = vermelho ;

Pais1 = amarelo ,
Pais2 = Pais5 = verde ,
Pais3 = vermelho ,
Pais4 = azul ;

Pais1 = amarelo ,
Pais2 = verde ,
Pais3 = Pais5 = vermelho ,
Pais4 = azul ;

Pais1 = amarelo ,
Pais2 = vermelho ,
Pais3 = Pais5 = azul ,
Pais4 = verde ;

Pais1 = amarelo ,
Pais2 = Pais5 = vermelho ,
Pais3 = azul ,
Pais4 = verde ;

Pais1 = amarelo ,
Pais2 = vermelho ,
Pais3 = Pais5 = verde ,
Pais4 = azul ;

Pais1 = amarelo ,
Pais2 = Pais5 = vermelho ,
Pais3 = verde ,
Pais4 = azul ;

Pais1 = vermelho ,
Pais2 = Pais5 = amarelo ,
Pais3 = azul ,
Pais4 = verde ;

Pais1 = vermelho ,
Pais2 = amarelo ,
Pais3 = Pais5 = azul ,
Pais4 = verde ;

Pais1 = vermelho ,
Pais2 = Pais5 = amarelo ,
Pais3 = verde ,
Pais4 = azul ;

Pais1 = vermelho ,
Pais2 = amarelo ,
Pais3 = Pais5 = verde ,
Pais4 = azul ;

Pais1 = vermelho ,
Pais2 = azul ,
Pais3 = Pais5 = amarelo ,
Pais4 = verde ;

Pais1 = vermelho ,
Pais2 = Pais5 = azul ,
Pais3 = amarelo ,
Pais4 = verde ;

Pais1 = vermelho ,
Pais2 = Pais5 = azul ,
Pais3 = verde ,
Pais4 = amarelo ;

Pais1 = vermelho ,
Pais2 = azul ,
Pais3 = Pais5 = verde ,
Pais4 = amarelo ;

Pais1 = vermelho ,
Pais2 = verde ,
Pais3 = Pais5 = amarelo ,
Pais4 = azul ;

Pais1 = vermelho ,
Pais2 = Pais5 = verde ,
Pais3 = amarelo ,
Pais4 = azul ;

Pais1 = vermelho ,
Pais2 = verde ,
Pais3 = Pais5 = azul ,
Pais4 = amarelo ;

Pais1 = vermelho ,
Pais2 = Pais5 = verde ,
Pais3 = azul ,
Pais4 = amarelo ;

Pais1 = verde ,
Pais2 = Pais5 = amarelo ,
Pais3 = azul ,
Pais4 = vermelho ;

Pais1 = verde ,
Pais2 = amarelo ,
Pais3 = Pais5 = azul ,
Pais4 = vermelho ;

Pais1 = verde ,
Pais2 = Pais5 = amarelo ,
Pais3 = vermelho ,
Pais4 = azul ;

Pais1 = verde ,
Pais2 = amarelo ,
Pais3 = Pais5 = vermelho ,
Pais4 = azul ;

Pais1 = verde ,
Pais2 = azul ,
Pais3 = Pais5 = amarelo ,
Pais4 = vermelho ;

Pais1 = verde ,
Pais2 = Pais5 = azul ,
Pais3 = amarelo ,
Pais4 = vermelho ;

Pais1 = verde ,
Pais2 = Pais5 = azul ,
Pais3 = vermelho ,
Pais4 = amarelo ;

Pais1 = verde ,
Pais2 = azul ,
Pais3 = Pais5 = vermelho ,
Pais4 = amarelo ;

Pais1 = verde ,
Pais2 = vermelho ,
Pais3 = Pais5 = amarelo ,
Pais4 = azul ;

Pais1 = verde ,
Pais2 = Pais5 = vermelho ,
Pais3 = amarelo ,
Pais4 = azul ;

Pais1 = verde ,
Pais2 = vermelho ,
Pais3 = Pais5 = azul ,
Pais4 = amarelo ;

Pais1 = verde ,
Pais2 = Pais5 = vermelho ,
Pais3 = azul ,
Pais4 = amarelo ;

no

| ?-

COMENTÁRIO FINAL

Assim sendo é possível verificar que atrvés da pergunta: colorir(Pais1,Pais2,Pais3,Pais4,Pais5).
foram encontradas várias combinações de cores possíveis de serem utilizadas na coloração do mapa em questão satisfazendo assim o objetivo do projeto.